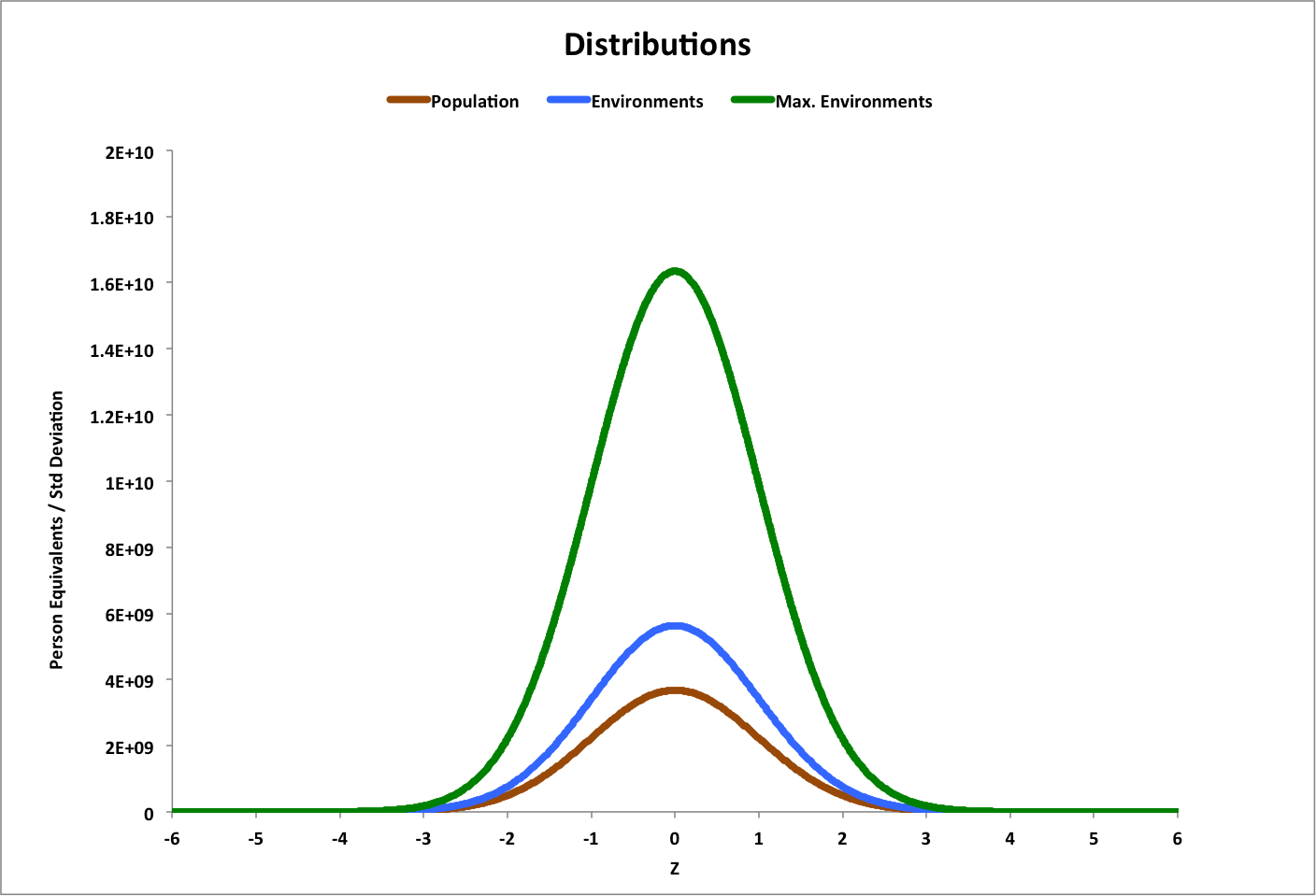
People and the environments they can inhabit are modeled as statistical distributions, each with their own population. They appear to be normal distributions. In the graph, Z is in sigma (standard deviations) centered on the people distribution, and population is the area under each curve.
The environments we inhabit are part of a larger, maximum set of environments. As our population grows, the number of inhabited environments grows until it reaches the maximum number available.
Over any given range of Z, the happiness (H) of the people (P) within it is the fraction of overlap between people and the environments (E) within the range:
H = MIN(P, E) / MAX(P, E)
Where the number of maximum environments (Emax) is greater than the number of inhabited environments (Epop), the average happiness (h) is the ratio of total population (Ppop) to inhabited environments:
h = Ppop/Epop
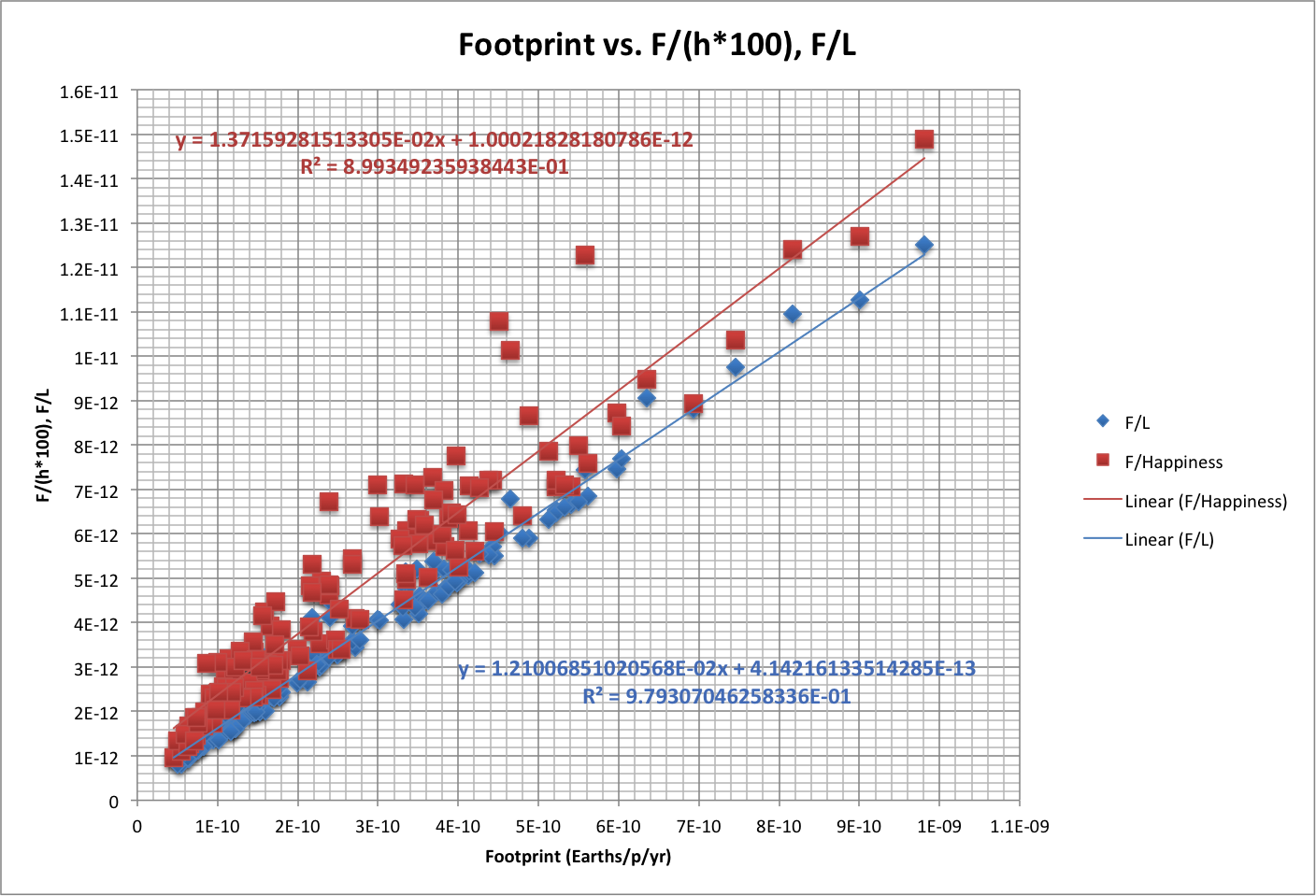
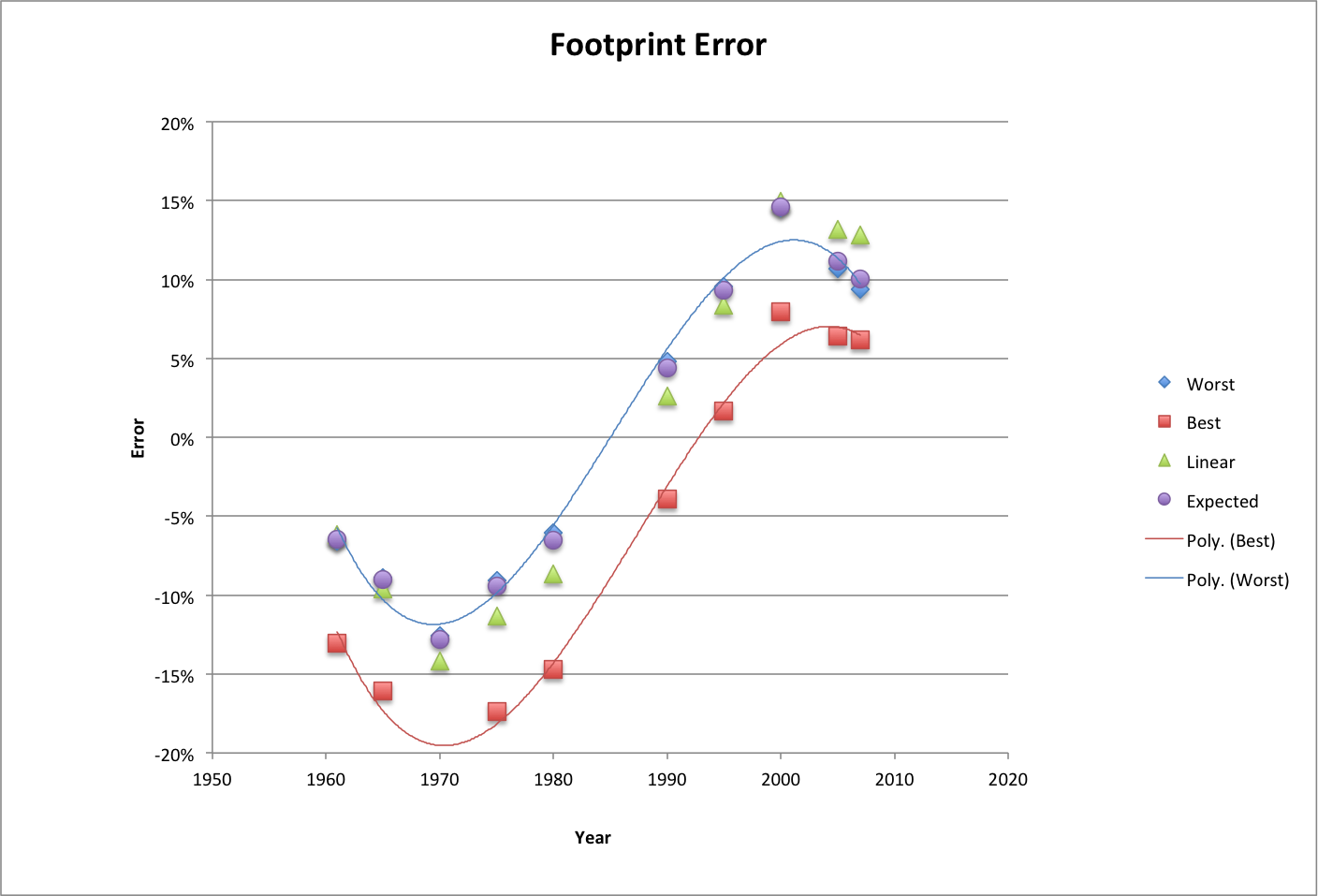
Based on data from the New Economy Foundation, which tracks happiness along with ecological footprint and other variables, happiness and life expectancy vary with ecological footprint F in a predictable way.
Using world data over time to find the best matches to these equations:
| F/h = | 1.22E+00 | * F + | 7.23E-11 |
| F/L = | 2.79E-03 | * F + | 2.90E-12 |
where F is in Earths/person/year, h is a fraction, and L is life expectancy in years.
These relationships show that both h and L asymptotically approach a maximum value as more ecological resources are expended. For h, this value is hmax = 0.82; for L it is Lmax = 358 years.
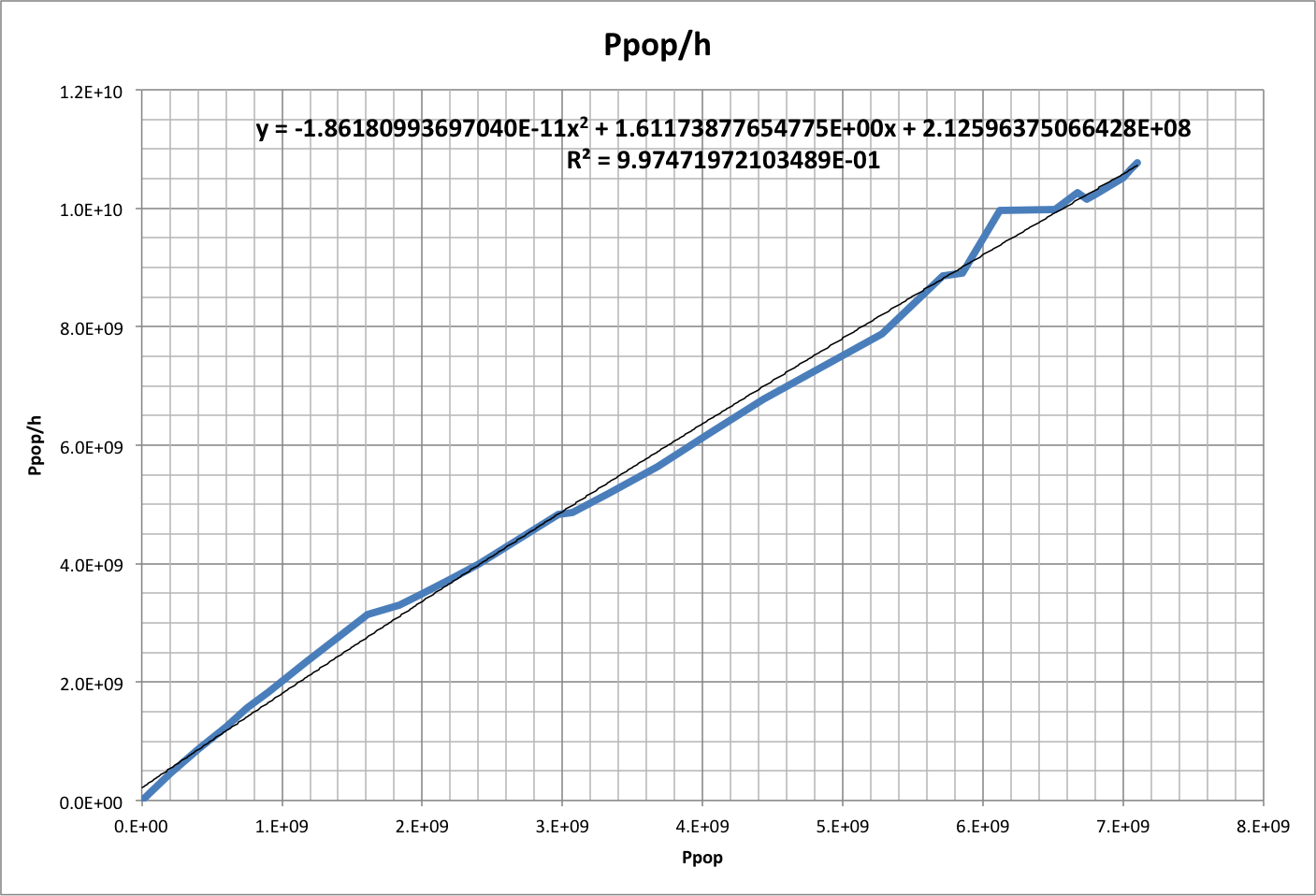
World (people) population varies in a similar way with happiness, as seen when happiness is projected over history based on the derived F/h and F/L relationships.
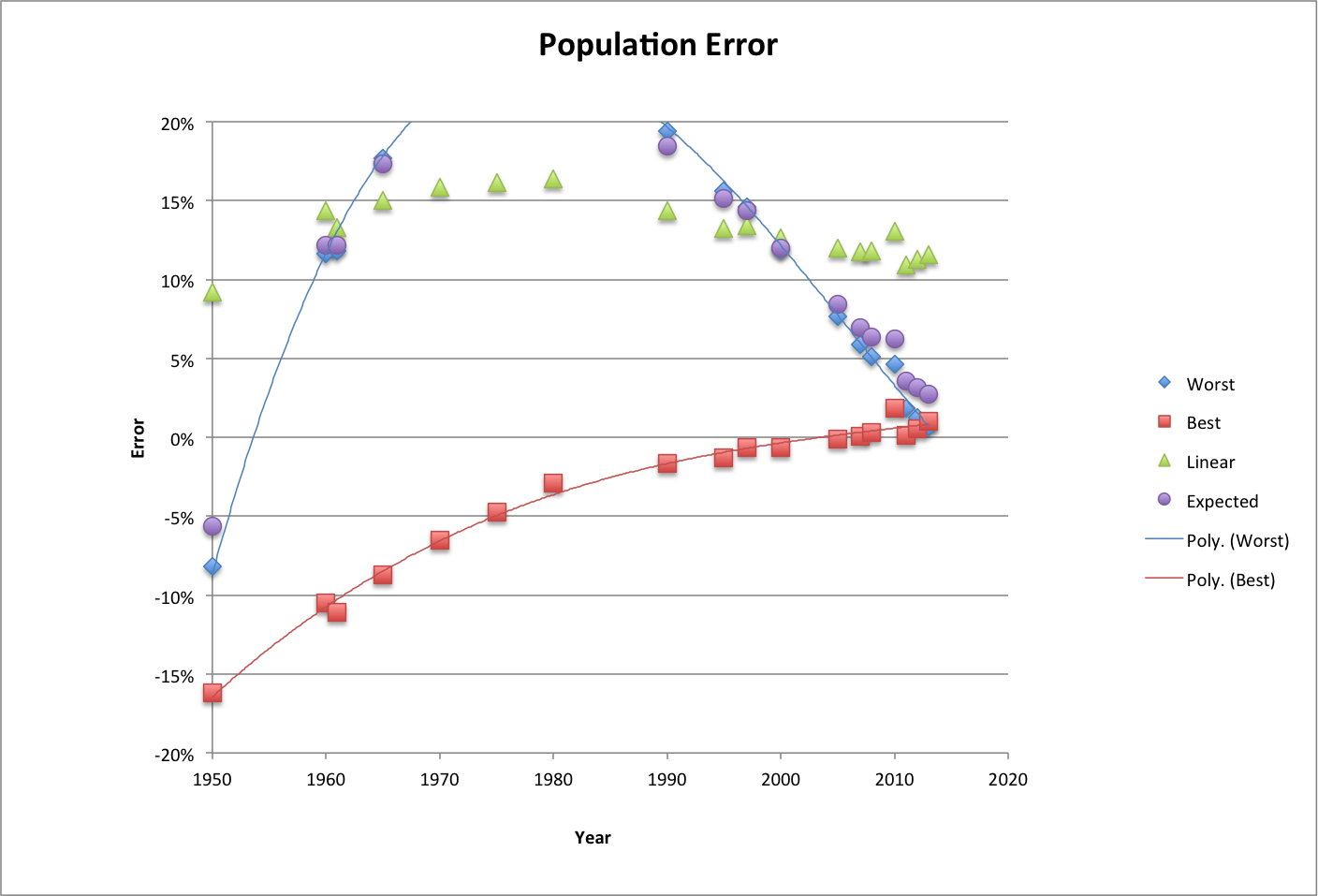
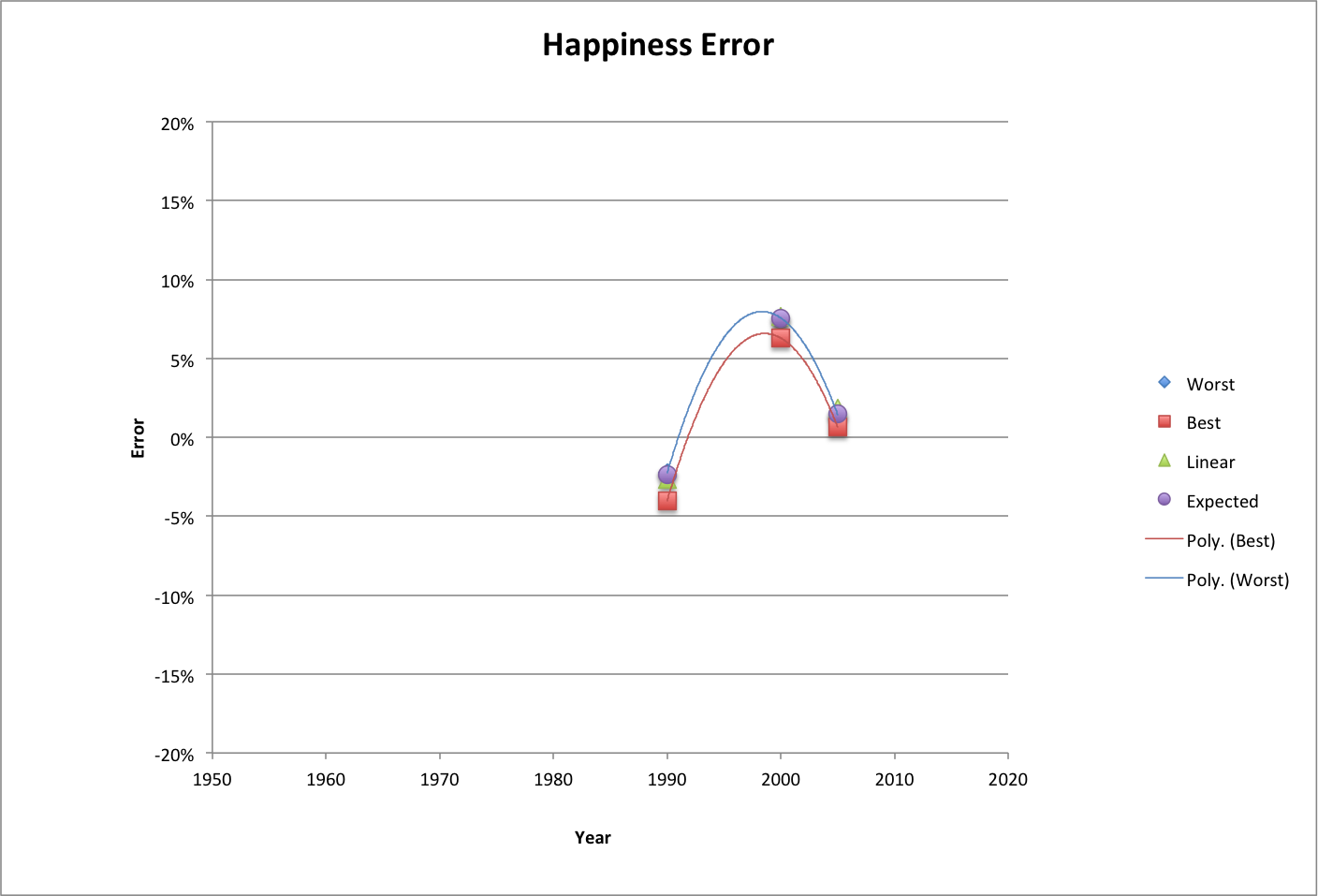
Following is the population error for this curve fit over the years 1-2013, which mostly represents the differences in the methods used to calculate happiness:
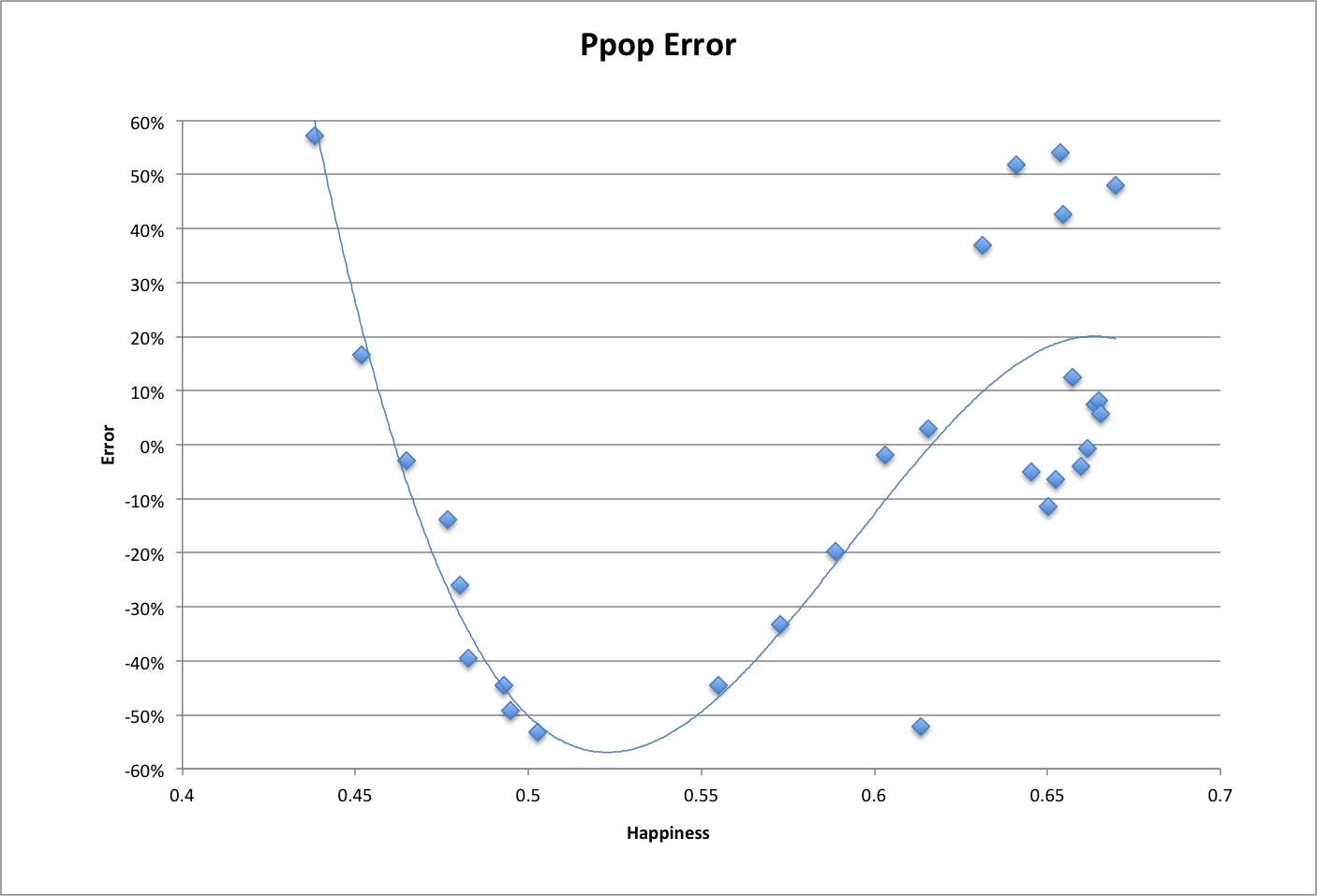
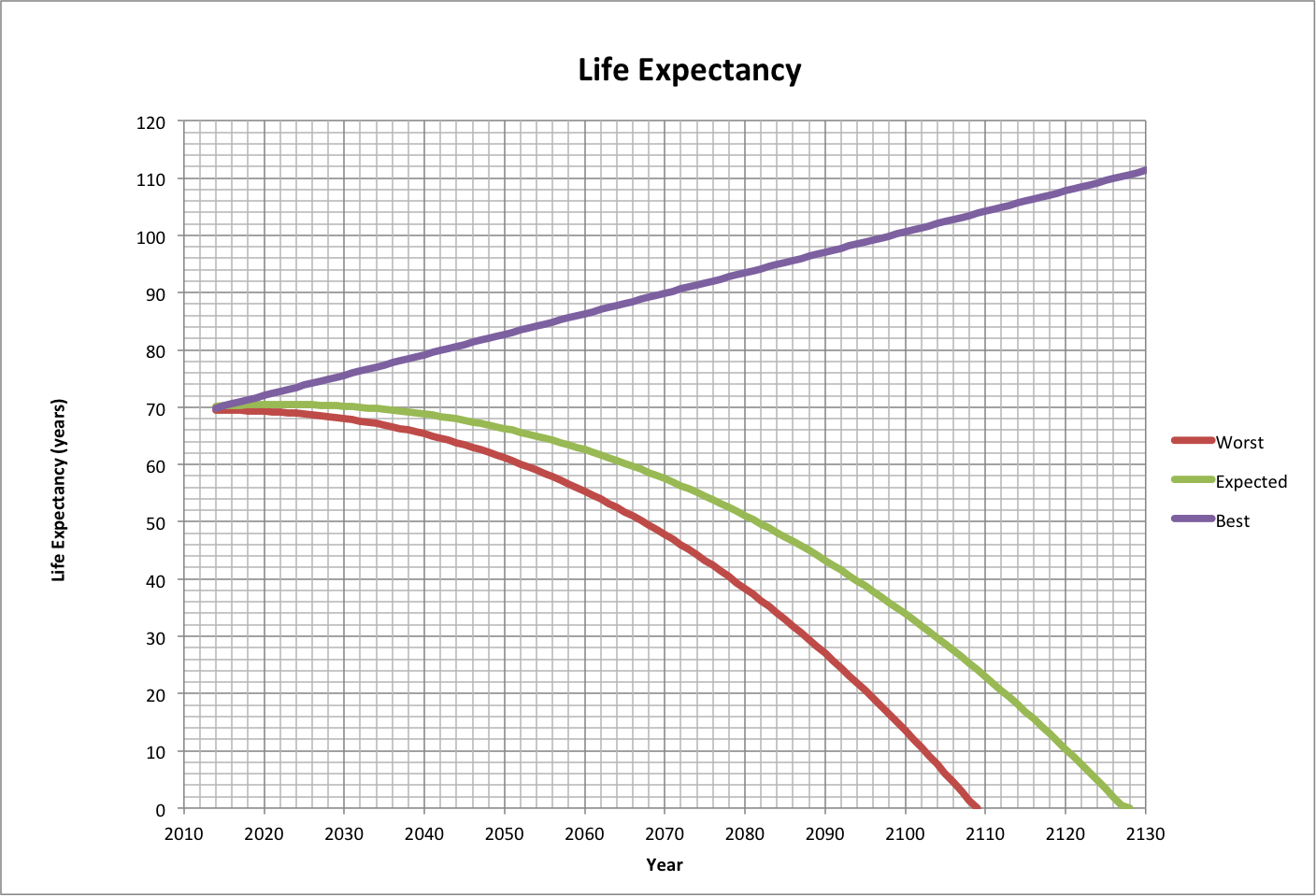
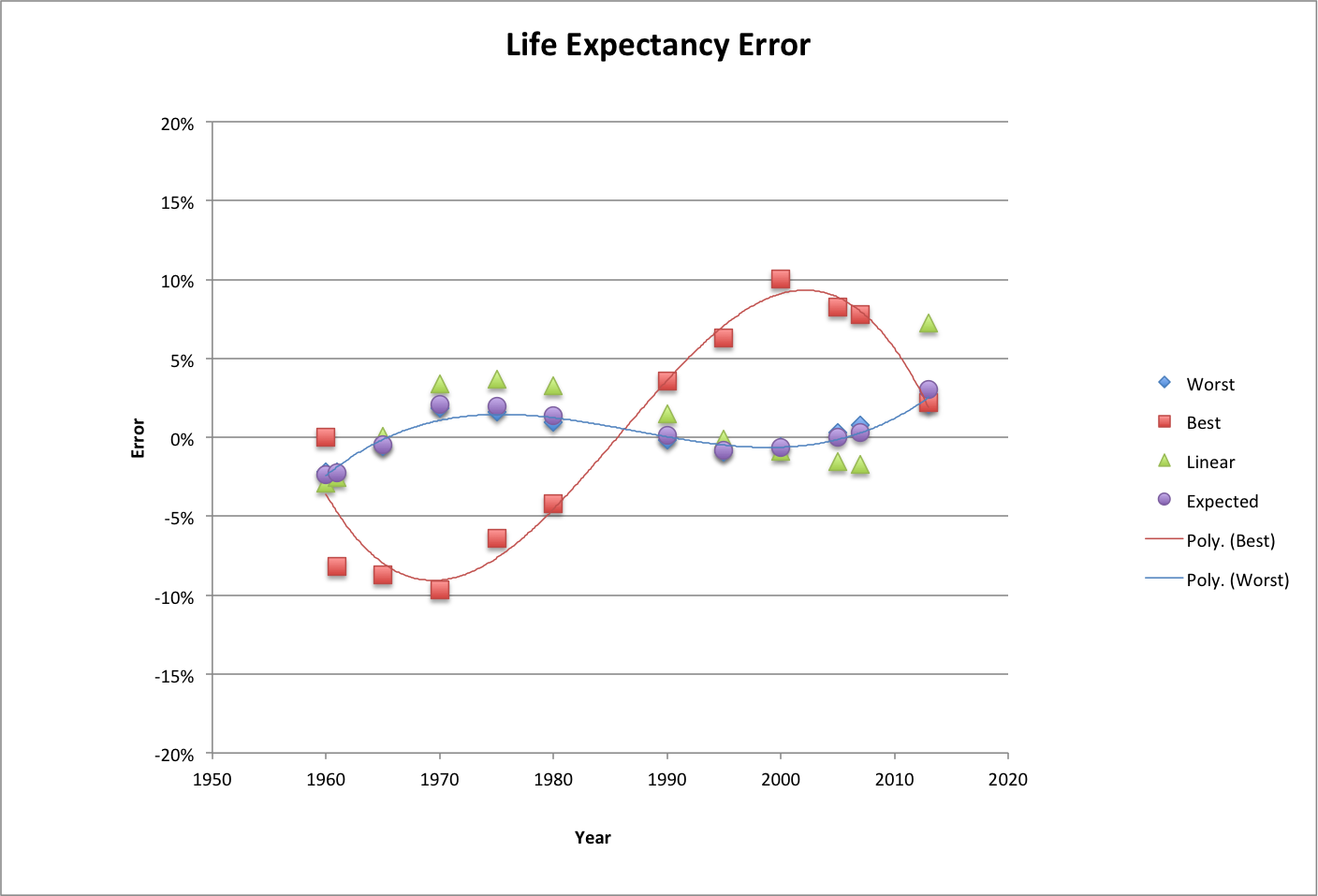
For a number of reasons, life expectancy can be used more easily than happiness in making projections into the future. Among those reasons, it is a larger and more observed variable and is linearly related to happiness.
Using polynomial curve fits to life expectancy over the period where footprint and life expectancy data is available, three scenarios have been chosen using coefficients of a third-order polynomial. Where t is the year:
| Worst L= | -1.83E-05 | * t^3 + | 1.04E-01 | * t^2 + | -1.98E+02 | * t + | 1.25E+05 |
| Best L= | 0 | * t^3 + | 0 | * t^2 + | 3.57E-01 | * t - | 6.50E+02 |
| Exp. L= | -1.22E-05 | * t^3 + | 6.89E-02 | * t^2 - | 1.29E+02 | * t + | 8.01E+04 |
The Expected case is a PERT estimate using least-mean-squares linear, second-order, and third-order curve fits. The Worst case is the third-order curve fit; and the Best case uses the slope of the linear curve fit, with the slope (-6.47E+02) adjusted to match the actual value for 2013.
NOTE: The coefficients shown above are rounded. Higher precision values are used to generate the graphs.
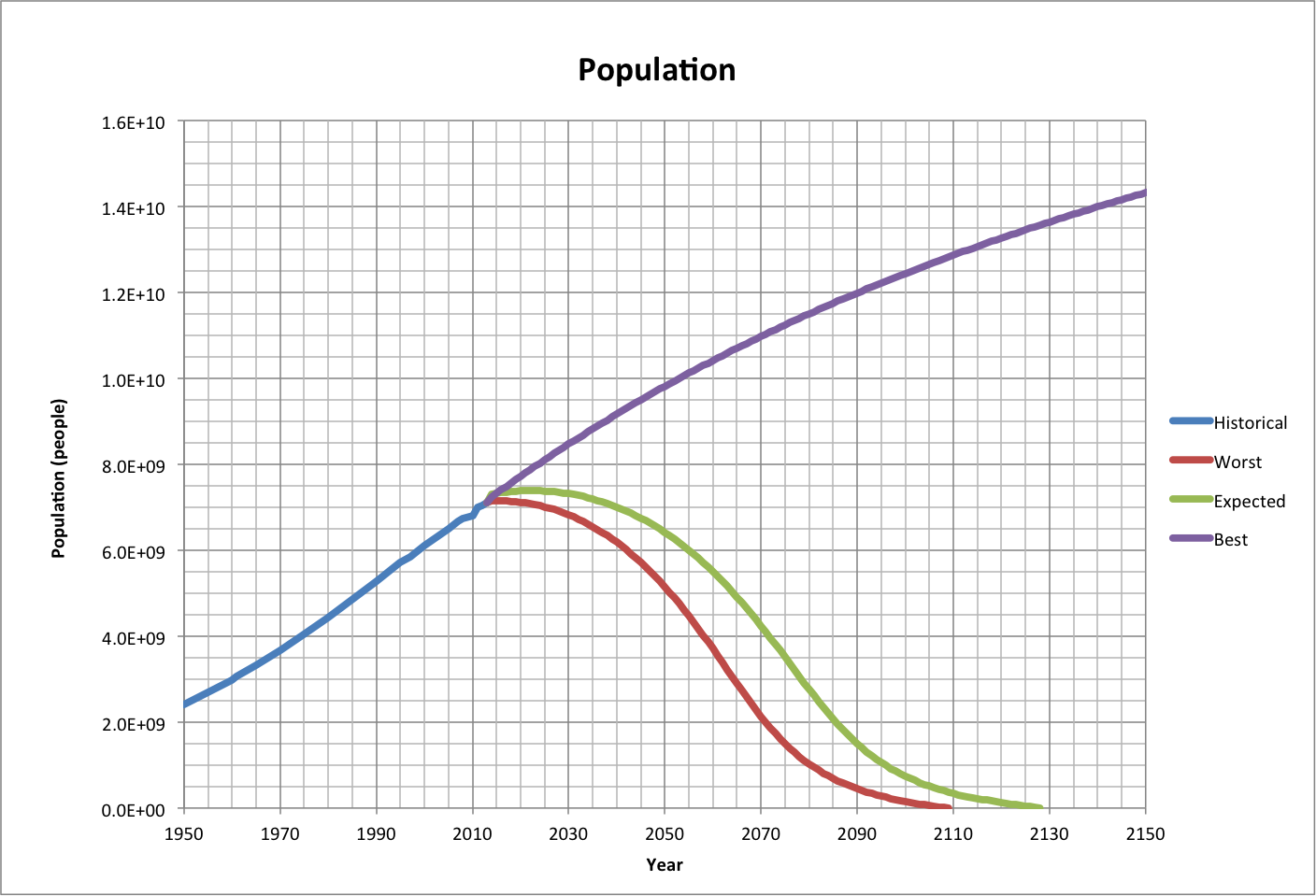
As with life epectancy, the Worst and Expected cases for world population technically reach a maximum ("peak") within the next decade, and drop to zero by early in the next century.
The Best case population continues to increase until 2821, reaching a maximum of 21.6 billion people as the happiness maximum is approached.
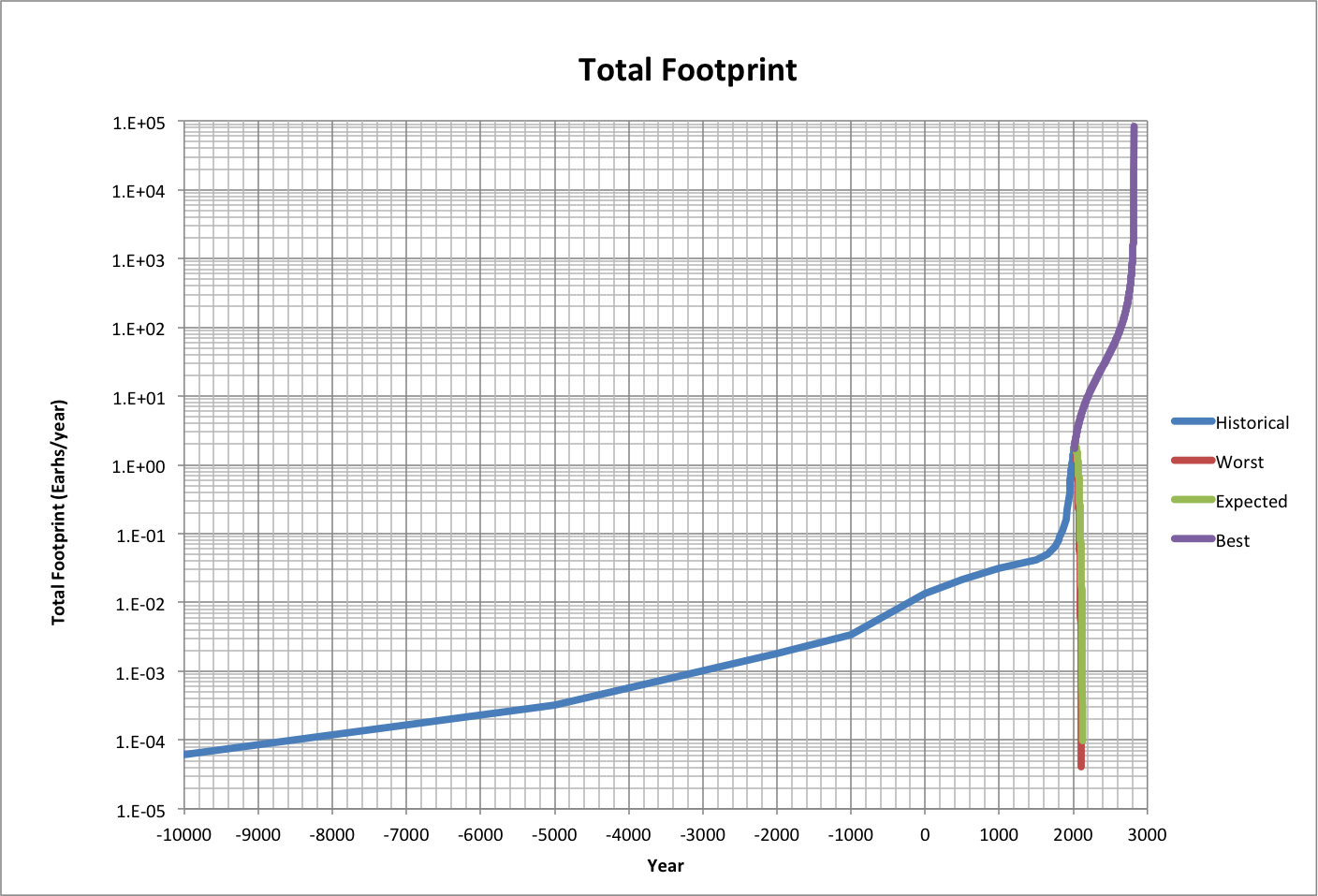
Projecting total ecological footprint (footprint per person times population) over time, the cost of increasing happiness is clearly prohibitive. The Worst and Expected cases peak at 1.79 and 1.88 Earths, respectively. In 2014, the total footprint is projected by the Worst case to be effectively at its peak. The Best case requires over 84,000 Earths at the beginning of the year (2821) that it gets closest to the maximum.
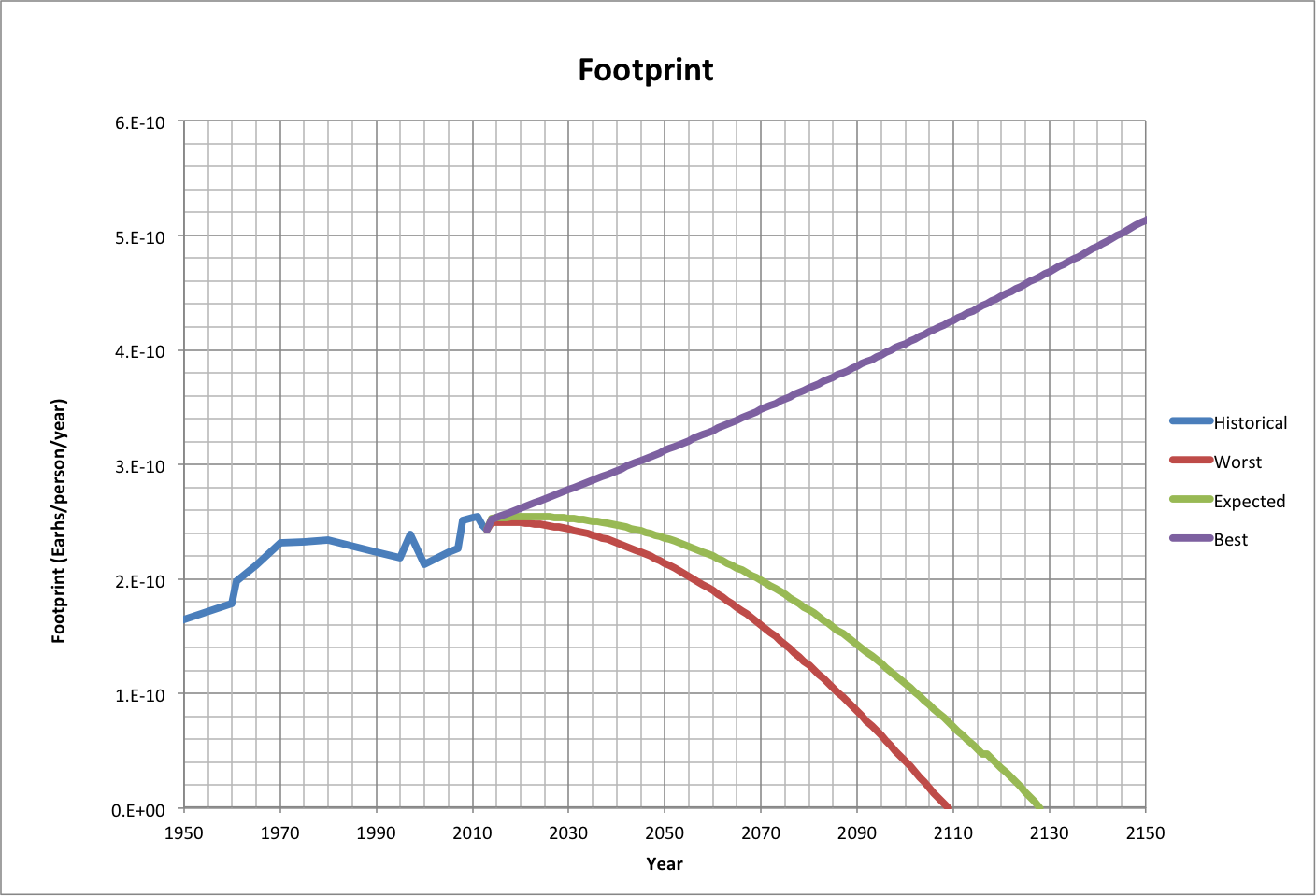 |
Footprint is estimated to have risen from 6.1E-11 Earth/person/year to 2.5E-10 in 2014. It will either peak near this value and drop, or continue increasing to 3.9E-06 by the beginning of the Best case's maximum year. |
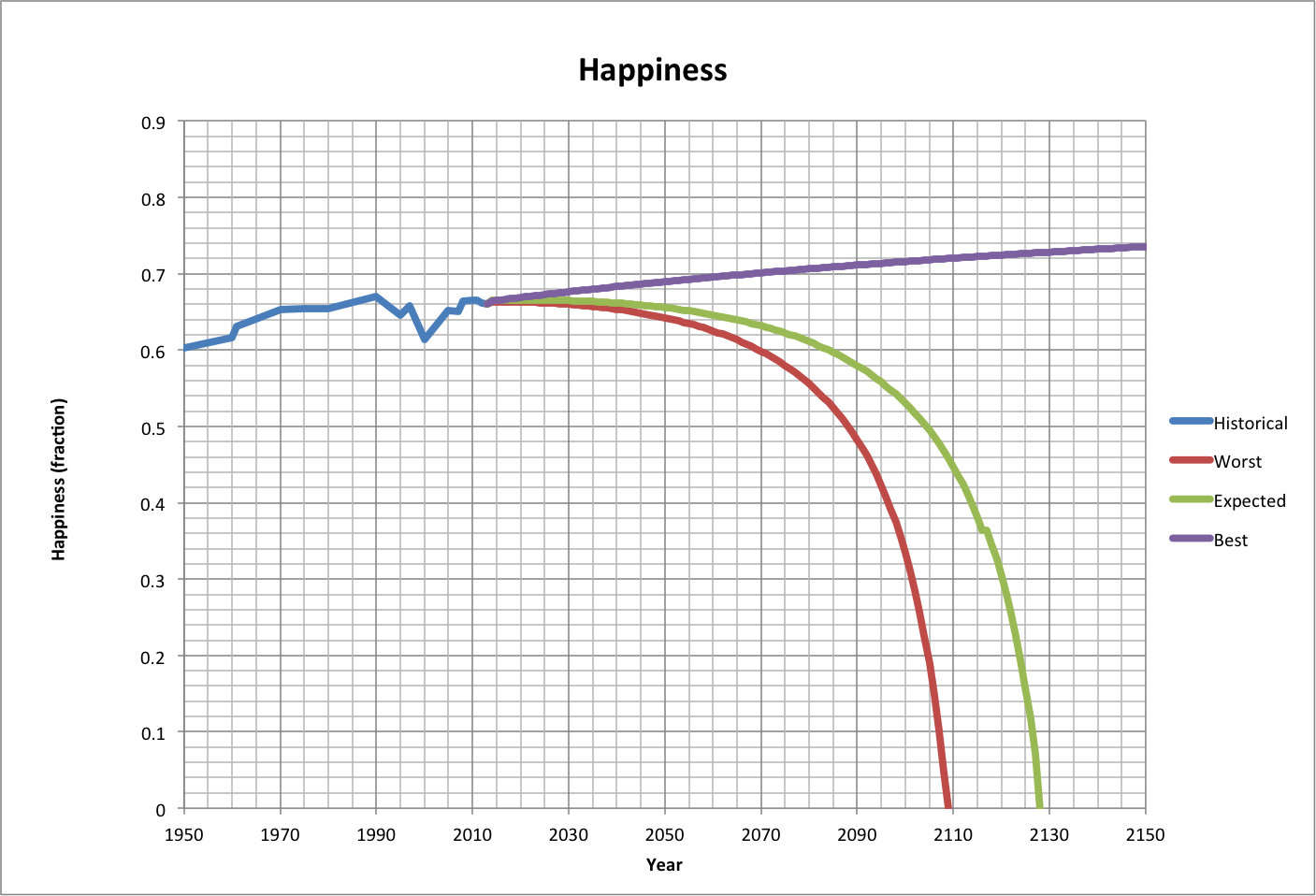
While the maximum happiness, approached in the Best case, is 0.82 (or "hmax"), the Worst and Expected cases both peak at nearly the same value (0.66).
The following sources were used to construct historical data:
| Source | Author/Link | Variable(s) | |
|
|
||
|
|
||
|
|
||
|
|
||
|
|
|
|
|
|
||
|
|
||
|
|
|
|