Priority Interdependencies

Based on models of task progress, population and consumption, and priorities, the following relationships are assumed:

Relationship Definitions

hself = F / ( uh * F + Fmin ) = Env / Envtot
  • hself = personal happiness (fraction)
  • F = per-capita ecological footprint (consumption of ecological resources in Earths/year per person)
  • Fmin = minimum ecological footprint
  • uh = constant
  • Env = occupied environments
  • Envtot = total environments
Fe = P * F
  • Fe = global footprint (consumption of ecological resources in Earths/year)
  • P = population (people)
h = i4 * Fe4 - i3 * Fe3 + i2 * Fe2 + i1 * Fe
  • h = group (average) happiness
  • in = constants

Lself = F / ( uL * F + frate )

 
  • Lself = personal longevity (years)
  • frate = constant (footprint/year)
  • uL = constant
Ltot = [ FeTotal - ( Fe + FeMin ) ] / ( dFe/dt )
  • Ltot = longevity of humanity (years)
  • FeTotal = Fe where species population S = 0
  • FeMin = P * Fmin
  • dFe/dt = Fe rate of increase (global footprint/year)
S = -b1 * Fe + b0
  • S = typical population of other species (fraction)
  • bn = constants
Lspecies = ( FeTotal - Fe ) / ( dFe/dt )
  • Lspecies = typical longevity of other species
Q = 1 - (1 - E )t/tmin
  • Task quality achieved (fraction of total)
  • E = efficiency (fraction)
  • t = time
  • tmin = minimum time to complete task (Q = 1, E = 1)
SUM(Prioritygoal)1 to g = (1 - Priority0)g
  • SUM(Prioritygoal)1 to g = sum of priorities
  • Prioritygoal = priority of goal
  • g = current goal (integer), where g < G
  • G = maximum goals (integer)
  • Priorityrawg = priority of goal if only a single goal (raw priority)
  • Priorityg = Priorityrawg * [ 1 - SUM(Prioritygoal)1 to g -1 ]
  • PriorityG = 1 - SUM(Prioritygoal)1 to G -1
  • Priority0 = value of Priority1  if all Priorityraw are the same
Qgoal = 1 - ( 1 - Egoal )T
  • Qgoal = fraction of goal achieved
  • Egoal = efficiency in attaining goal
  • T = Prioritygoal* t / tmingoal
  • tmingoal = minimum time to reach a goal (Qgoal = 1, Egoal = 1)
Effect = [ (P - N) * XP + N * XN ] / P
  • Effect = net result of new change and old trend
  • XN = Variable value for number of people N
  • XP = Variable value for number of people P - N

 

Key aspects can be summarized by the following rules of thumb:

INCREASE

TO DO THIS
  • Footprint (F)
  • Increase personal happiness (hself)
  • Increase personal longevity (Lself) to maximum, decrease afterward
  • Footprint (F)
  • Population (P)
  • Increase others happiness (h) to maximum, decrease afterward
  • Decrease others longevity (Ltot)
  • Decrease species population (S)
  • Decrease species longevity (Lspecies)
  • Increase required ecological resources (FeMin)
  • Total ecological resources (FeTotal)
  • Increase supportable population (P)
  • Increase others longevity (Ltot)
  • Increase species population (S)
  • Increase species longevity (Lspecies)
  • Goal priority
  • Decrease time to accomplish goal

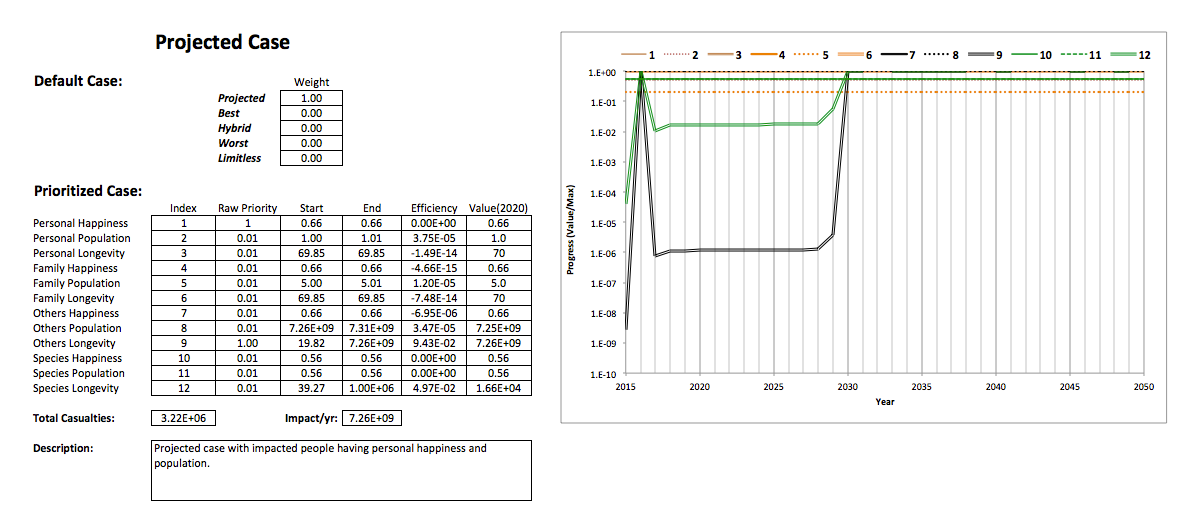
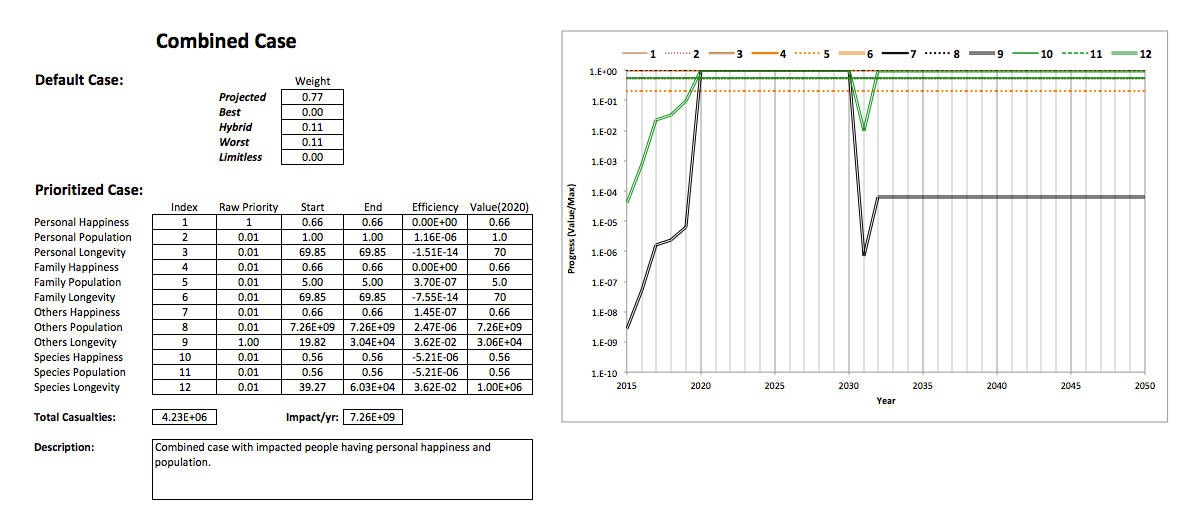
The following images show the results of simulations using several Half-World scenarios.

The total ecological resources are fixed at their current estimated value, and high priority is placed on others longevity, which is influenced by getting a number of people to adopt the same personal goals ("impact"). Graphs show the trajectories of progress for all goals (identified by index numbers) on a logarithmic scale, with each year marked at the middle of the year.
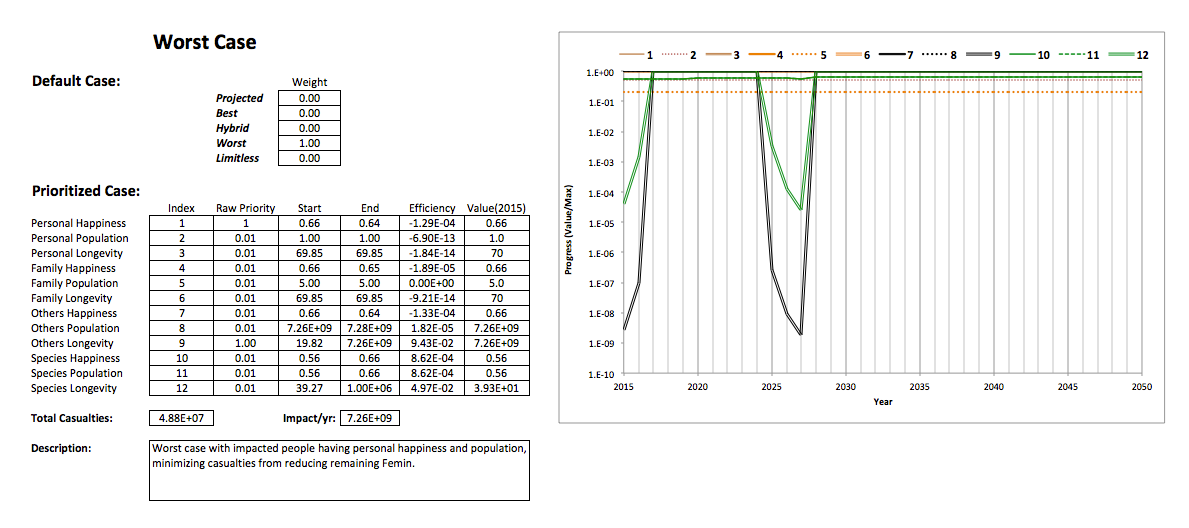
Limitless

Combined

Projected
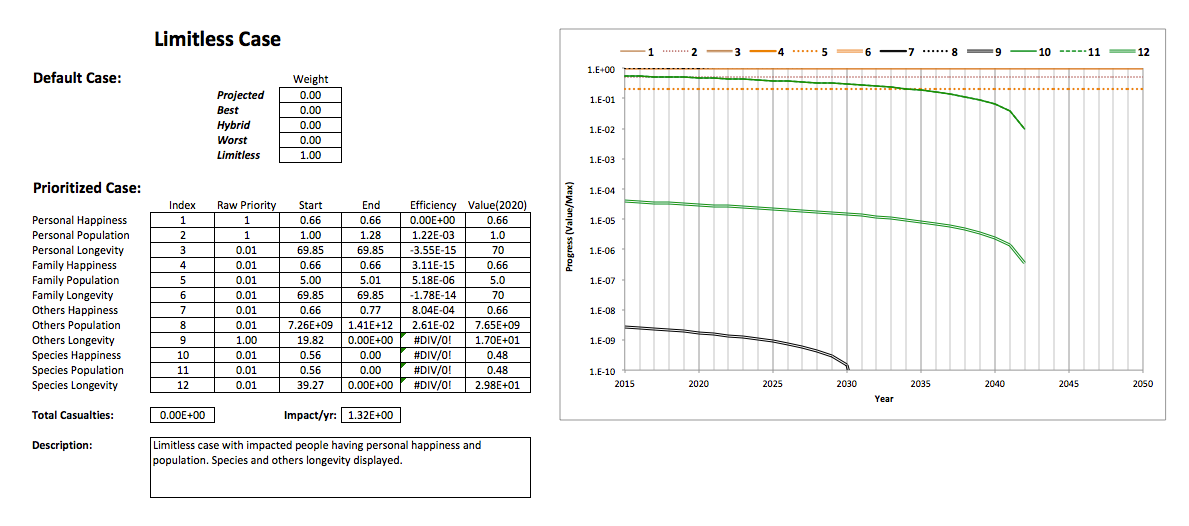
Worst
The following graph shows lives saved (difference in casualties) as a function of impact for the combined case:
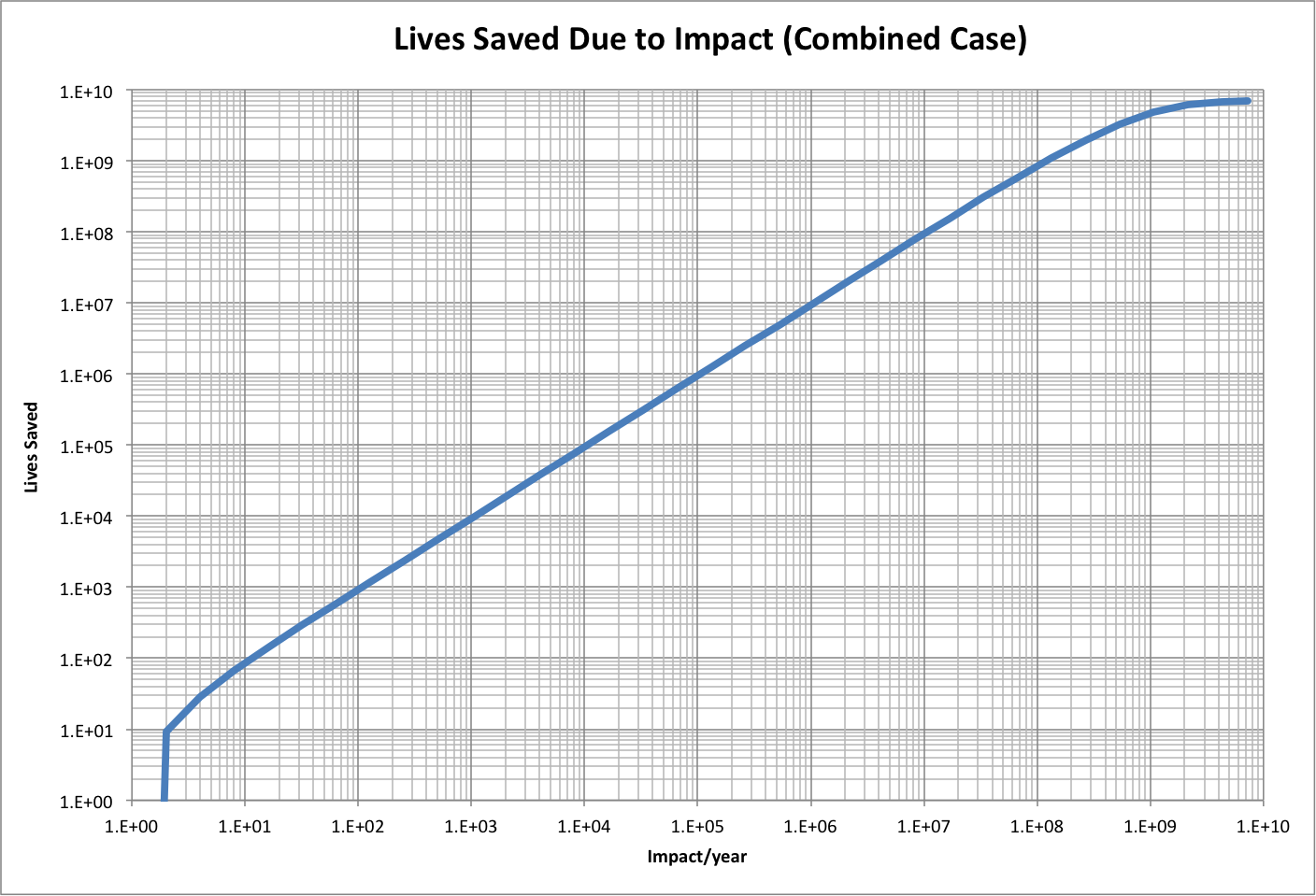
Saved Lives

 

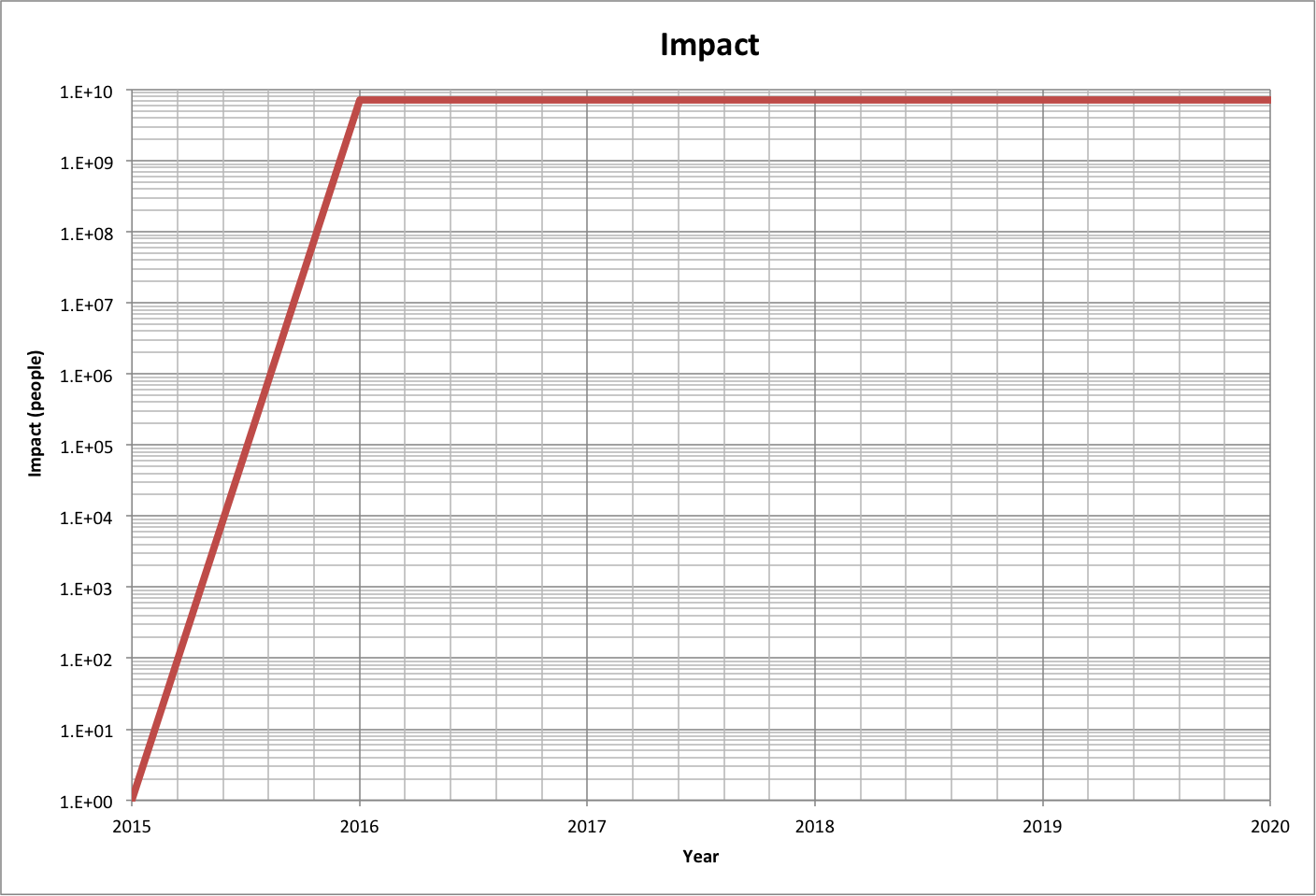
The following graph shows impact as a function of time for full effect (7.26E+09/yr):
Impact

While the graphs above assume that there is built-in impetus to follow the trajectories in the Half-World scenarios (which are modified by the changes due to priorities), the following graphs display how population and footprint are constrained if enough ecological resources are left to support the species we depend on for basic survival. That is, Fe + FeMin < FeTotal - FeMin, and therefore

  • Varying F, then P < [ Pcritical = FeTotal / ( F + 2 * Fmin ) ]
  • Varying P, then F < [ Fcritical = FeTotal / P - 2 * Fmin ]

The next graph begins with values of population (Pstart) and footprint (Fstart) in mid-2015, and plots

  • P vs. F = P / Pstart on X-axis, Fcritical / Fstart on Y-axis
  • F vs. P = F  / Fstart on X-axis, Pcritical / Pstart on Y-axis
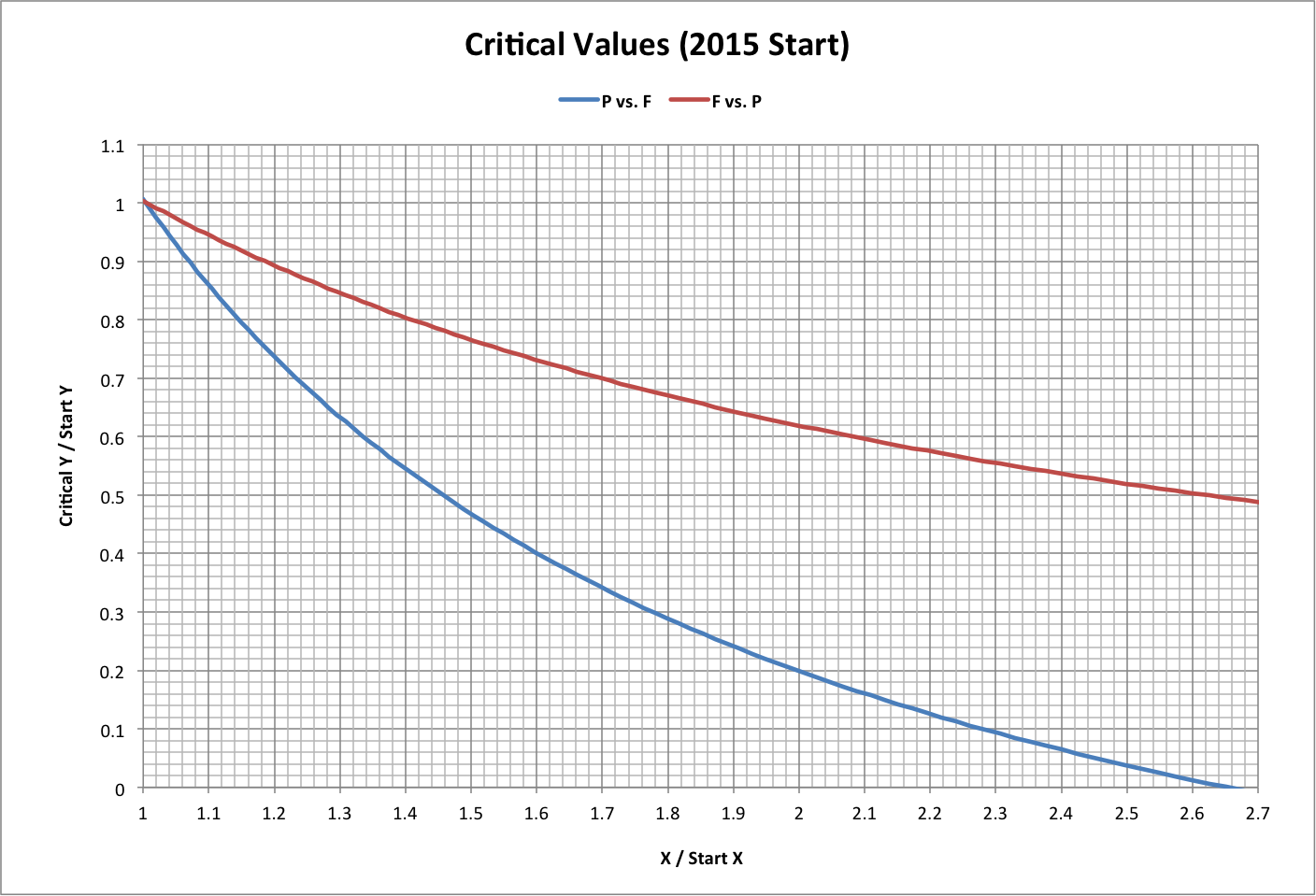
Critical Values (2015 Start)

 

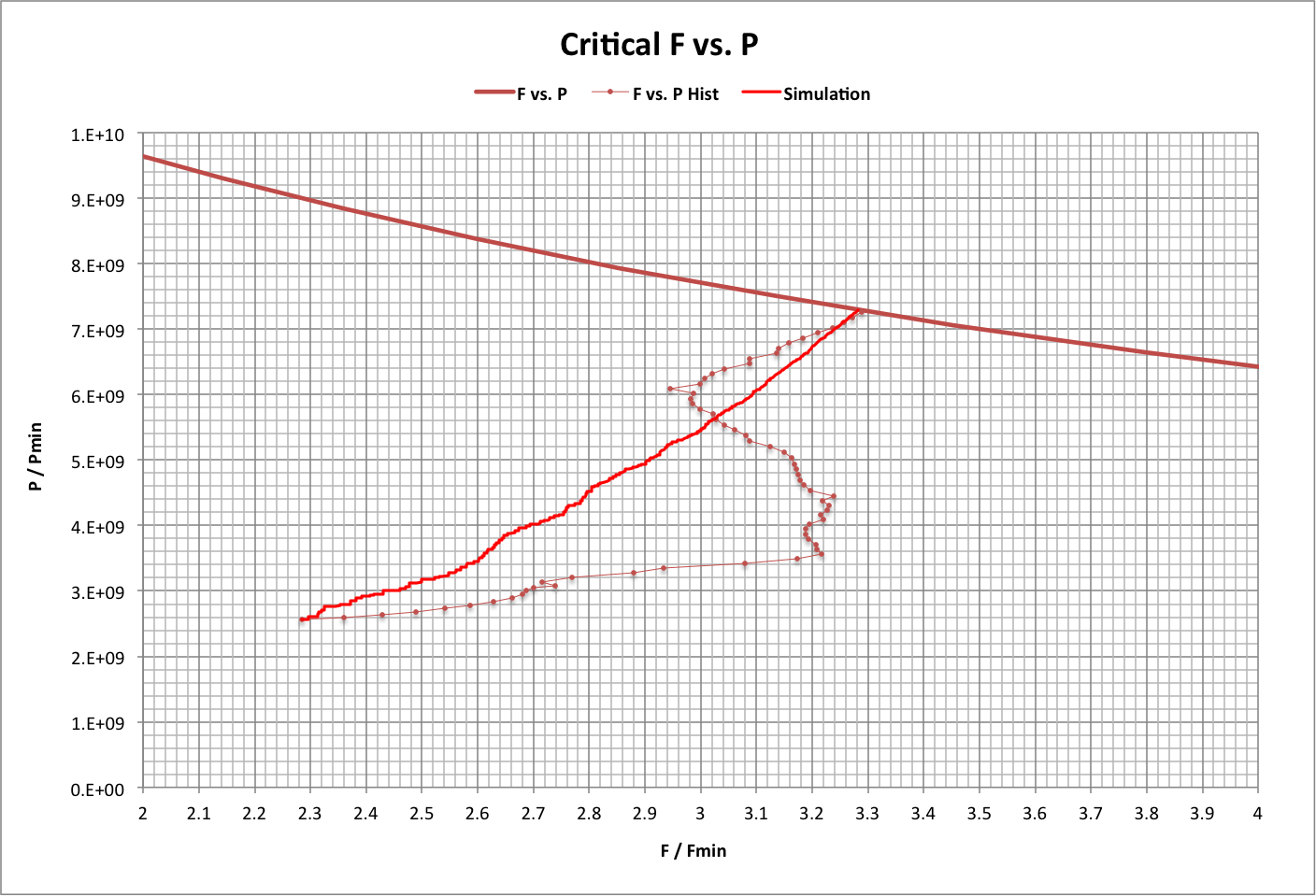
The following graph plots critical values of P and F as above, but over a broader range. Here, Pstart = 1 and Fstart = Fmin.

Note that, in 2015, P / Pstart = 7.26E+09 and F / Fstart = 3.29. Roll over the image for a close-up.

 

Corresponding happiness values are shown below, where

  • P vs. Critical h = P / Pstart on X-axis, happiness at Fcritical on Y-axis
  • F vs. h = F / Fstart on X-axis, happiness at F on Y-axis

Current (2015) happiness is 0.66.
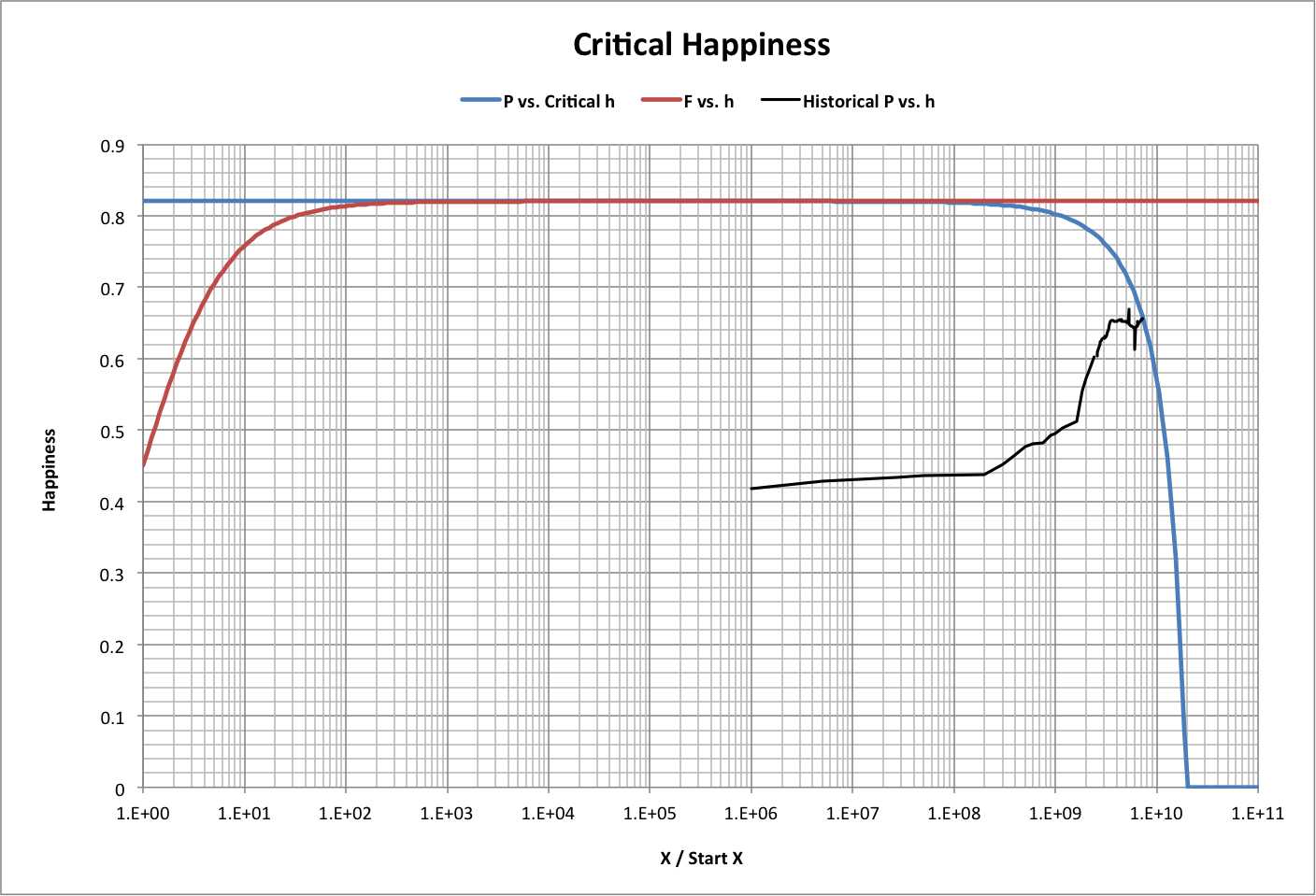
Critical Happiness

 

Historical values of footprint and population from 1950-2015 are superimposed on the critical values (with Pstart = 1, Fstart = Fmin) in the graph below. Roll-over the image to see P vs. F.

Also shown are results of a simulation that starts with F and P for 1950 and takes the following steps 2500 times:

  1. Calculate current F limit.
  2. Move F toward the limit as a fraction of the distance to it, with the fraction equal to a random number (between 0 and 1) times an efficiency of 0.002.
  3. Calculate the new P limit.
  4. Move P toward the limit as a fraction of the distance to it, with the fraction equal to a random number (between 0 and 1) times an efficiency of 0.01.

 

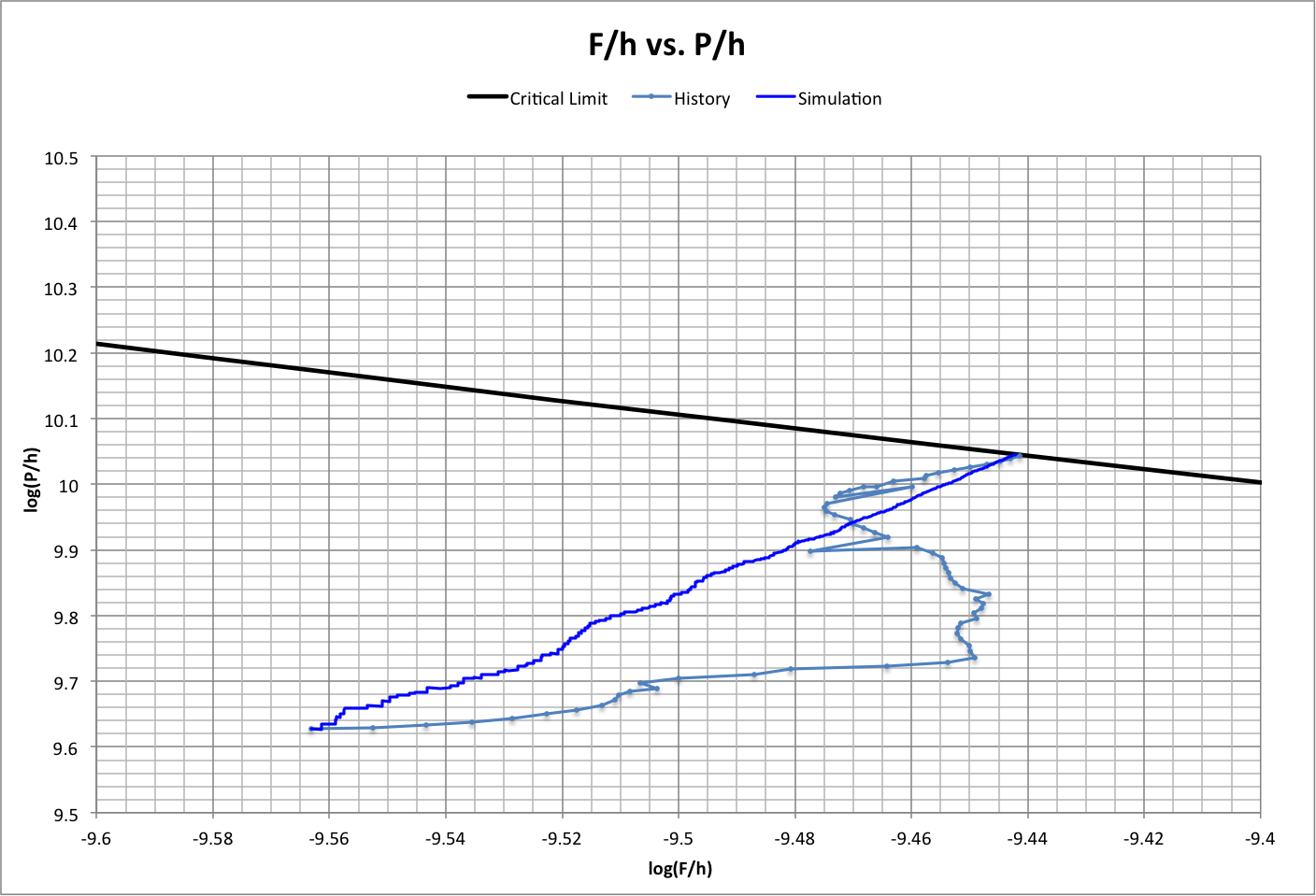
The following graph takes critical population values and calculates the corresponding critical footprints, then calculates happiness from the results to derive a plot like that used in the simulations of population and consumption used in version 4 of the Population-Consumption model.
Log Plot

 

For a discussion, see the following:

 
© Copyright 2015 Bradley Jarvis. All rights reserved.