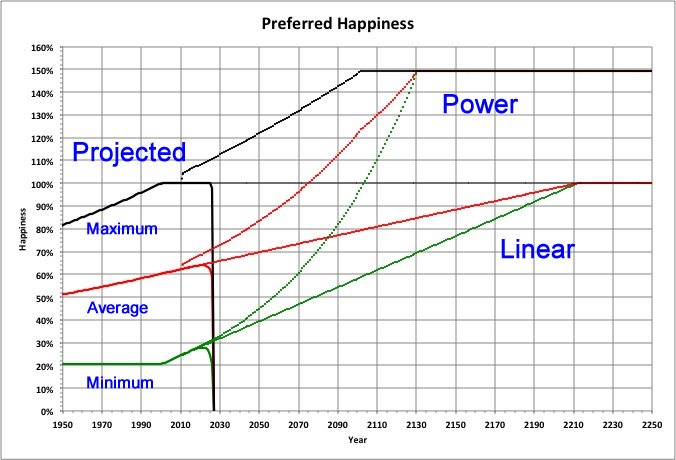
We can extrapolate historical increases in happiness to estimate what the world's population would prefer it to be in the future.
If happiness could increase linearly, the entire population would reach 100% happiness in 200 years.
Those at the upper limit would like it to increase beyond 100%. Optimistically, with the happiness trajectiories increasing as a power function and starting in 2011, transportation speed would be the limiting factor (here, the speed of light).
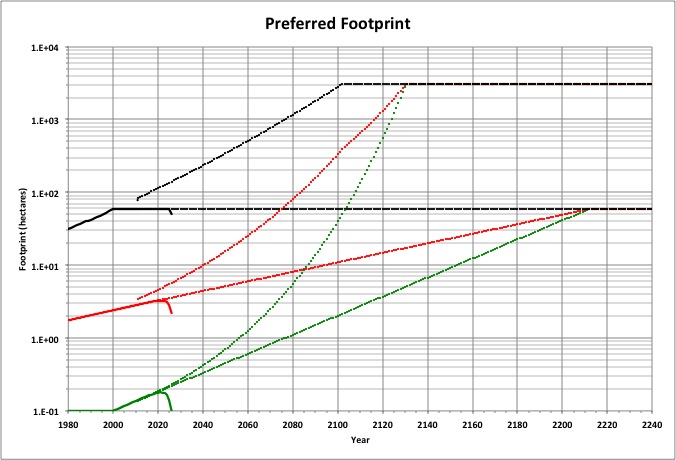
Preferred happiness translates into ecological footprint as shown, which is proportional to per-capita consumption and population.
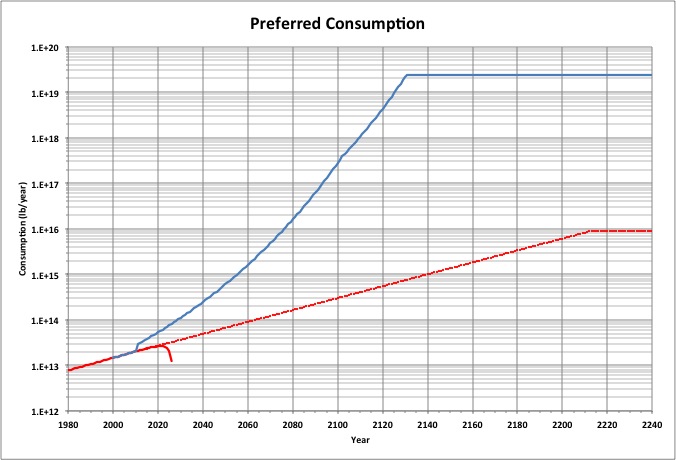
For the linear increase in happiness, total consumption would reach a maximum when 100% average happiness is achieved, and stay fixed at about 432 times its 2010 value (734 times what Nature can provide).
For happiness increasing as a power function, the population would ultimately be consuming nearly 2 millionths of the Earth's mass each year.
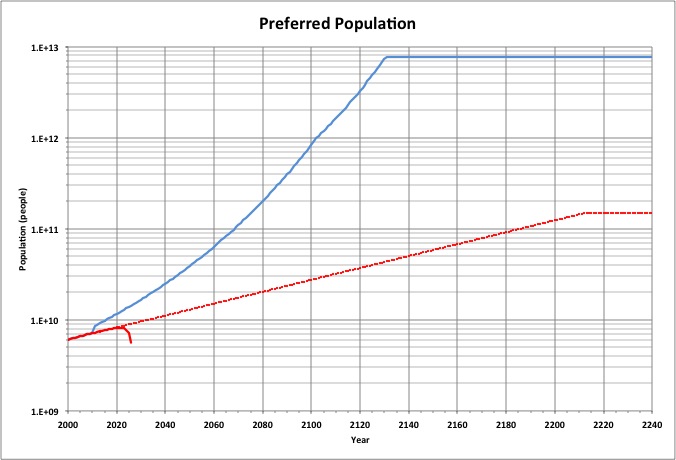
For the linear projection of happiness, the population would rise from 7 billion now to more than 148 billion, with a life expectancy of 101 years.
For the power projection, the population would reach a maximum of nearly 7.8 trillion, with a life expectancy of 140 years.
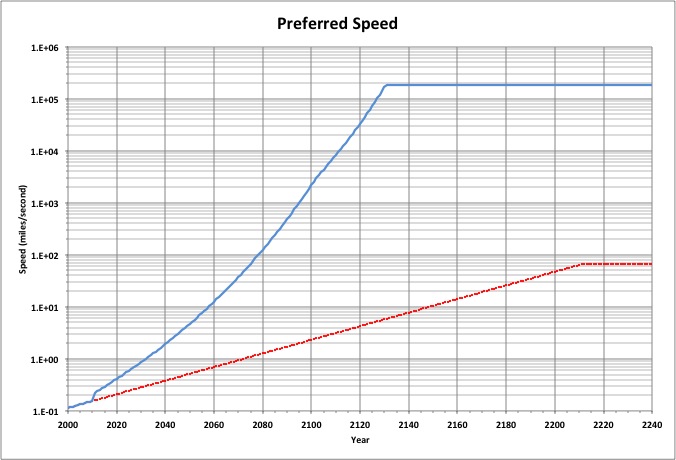
The average transport speed would rise in proportion to consumption.
When happiness is at its maximum, the speed would be more than 67 miles per second, several times the impact speed of an asteroid.
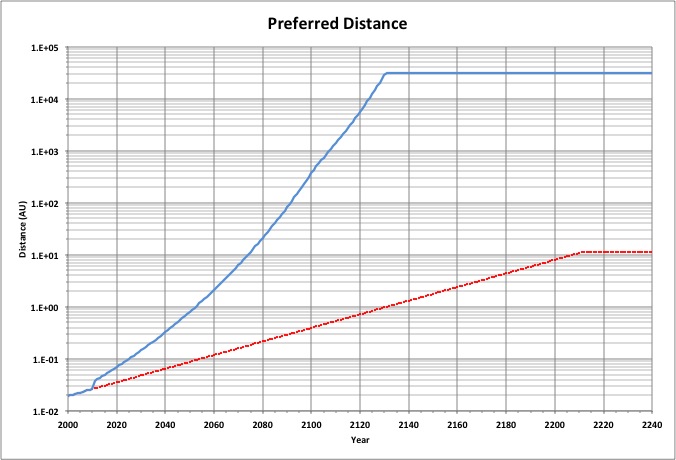
The greatest distance between two points conducting one transaction per year increases with consumption. Half that distance (shown) is the radius of a sphere encompassing all transactions.
For the linear projection of happiness, the sphere ultimately extends beyond Saturn's orbit. For the power projection, it extends a half a light year.