Future Alternatives

Version 1

I merged my two leading models of the relationship between resource consumption and population into one combined population model, which shows better than ever the constraints on future growth. The new model uses a generic definition of “resources,” measured in units of mass, and incorporates access to the resources and response to perceived depletion of resources into the mathematical description of consumption. Renewable resources (“capacity”) are counted as non-renewable resources which don’t begin to be depleted unless consumption exceeds the amount that is replaced.

We have several options:

(1) We can continue business-as-usual, which will result in a catastrophic depletion of resources associated with a population crash. The timing is the same as before, beginning with a population peak about 30 years from now.

(2) If we want to continue the growth in consumption and population we’re currently enjoying, we must access new resources by about 10% per year if we start in 2010. This growth can be sustained for a maximum of another 200 years, when we will be unable to move resources fast enough and will be forced to live with limited consumption.

(3) We could stop growth in overall consumption. Beginning in 2010, this would buy us another 30 years or so.

(4) If we could somehow decrease our consumption without adversely impacting population (for instance, by distributing resources to poor people so the reduction doesn’t kill them), then we could stretch our resources longer. If the minimum per capita consumption is what the average was in 0 A.D., then we could stretch our resources no more than about another 1,400 years if we start in 2010 (less if we start later).

(5) We can attempt to increase the amount of renewable resources to a level just above the consumption that could sustain a preferred population size and keep our consumption constant. We would use non-renewable resources only as necessary to adjust to changes in renewable resources (and help make those changes). Starting in 2010, I estimate that to avoid the impending population crash, we would need to increase renewable resources by at least 16% per year while keeping consumption constant. While theoretically we could do this indefinitely, we would only have two years' worth of non-renewable resources to handle contingencies.

(6) We could use a mixed strategy of growth and sustainability. This would involve simultaneously increasing our access to both renewable and non-renewable resources while restricting growth in consumption. I estimate that in the best case (keeping consumption constant) we could extend resources more than 1.6 million years.

Of the options for avoiding a reduction in population, the mixed strategy (option 6) seems to make the most sense. One way or another, the world will be forced to support its population with new resources within the next 20 years.

My model projects that if we continue our historical increase in consumption (the “No Change” scenario), we will use 46 times this year’s consumption between 2009 and the population peak in 2037. By the time of peak, 144% of this year’s population will be consuming 210% of the resources we will this year. If we are not currently increasing resources, we may need to devote part of our consumption to this task, effectively reducing population growth in the process.

If we focus on acquiring renewable resources, we will not need to continually add new resources to replace the amount that we use. We would get the most efficiency out of what we spend to get those resources, leaving remaining (and new) non-renewable resources for dealing with changes in conditions that might force alterations in infrastructure such as global warming.

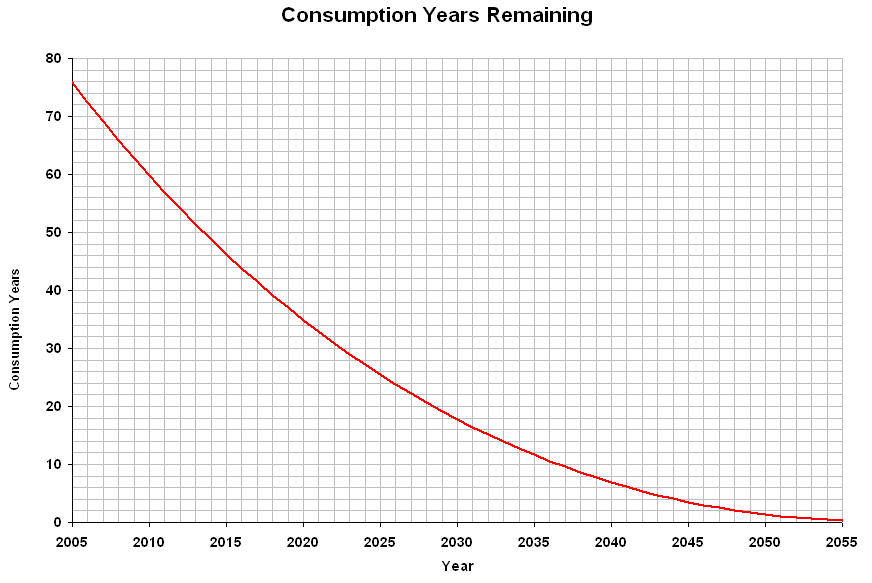
The following graph shows the remaining resources (in terms of number of years of consumption, or "consumption years") available for adding new resources if consumption is held constant. Note that after 2037, population declines.

The outcomes of my combined population model match my definition of “worlds” – practically isolated systems that people inhabit: A small population (less than one-hundredth the present number) living off the land and the scraps of our civilization; a population a little larger than ours, limited to the Earth and relying on totally renewable resources; or a much larger interplanetary population, limited to the Solar System and using entirely renewable resources; or a population that grows and then sheds people, by death or emigration, while consuming no more than a maximum amount of renewable resources.

The first world would result from using almost entirely non-renewable resources. It could be realized between 50 to 200 years from now, depending on whether and how fast we acquire new resources.

The second world would be the result of extremely rapid growth of renewable alternatives to energy and production, with us using entirely renewable resources within 60 years. No new non-renewable resources will have been found.

The specifics of the third world depend on how fast we can acquire new resources. For it to exist at all, we would need to have enough non-renewable resources to offset the depletion of non-renewable resources being used to support the population and eventually accounting for all of our consumption (likely within 400 years).

In each of these alternative worlds, people would be limiting themselves to what can be regenerated on an annual basis. The conflict we are currently experiencing between competitors and cooperators will be present in each of these worlds as they deal with the necessity to curb consumption to the renewable resources that are available. In these cases where the speed of travel is limited, there would be no more resources for use in expanding the population and keeping it coherent; we would all need to become cooperators or at least restrain the behavior of competitors.

The fourth world would come into existence if the need of competitors to acquire more resources from themselves could not be controlled. The competitors could then either leave to start other worlds (emigration) or be allowed to kill people. Because the efforts of everyone are necessary to sustain consumption, overall consumption would drop with population, and resources would then be available for growth. The world would cycle between growth and death, growth and emigration, or some combination of both.

I estimate that the world currently has 62% of the resources that it had in 0 A.D., a fraction that is decreasing by more than 1% annually. By the time it falls below 20%, less than 30 years from now, we will be forced to consume less each year, which will likely result in a decrease in population. If we are unable to increase the world’s supply of non-renewable resources to compensate for what we consume, then to avoid a loss of population we must increase our use of renewable resources.

This can be done by first deciding how much consumption we want to have (proportional to the square root of the population size we want). We could choose, for example, to freeze world consumption at what it will be in 2010, or we could choose to let it grow to twice the 2010 level. Once we are able to supply that amount by renewable resources, we won't be able to increase how much we use without increasing the supply.

Next, we need to decide when we will start increasing the amount of renewable resources that we use; keeping in mind that waiting longer will force us to work faster. If we start at the end of 2010, we will need to add about 1% each year to the fraction of consumption supplied from renewable resources (the “renewable fraction”) while keeping consumption constant at the 2010 level. If we wait until the end of 2020, holding consumption constant at that level, the renewable fraction will be nearly 2%. Waiting until 2030 increases the renewable fraction to almost 4%. By the population peak (2037), it will be too late to do anything.

The renewable fraction is proportional to the total amount of consumption that we choose as a maximum. With consumption limited to what it will be in 2010 and assuming we are not using any renewable resources, we will need to get 1% of what we consume from renewable resources in 2011. In 2012, we add 1% to get 2%; the following year, we add the renewable fraction to get 3%, and so on. If we choose instead to double the amount of consumption, the renewable fraction doubles to 2% per year; we are still starting to increase our amount of renewable consumption at the end of 2010, but we are allowing consumption to grow as it has until it reaches the limit (around 2031). Note that for any given year, using the previous year's consumption to determine how much renewable resources we will use will reduce the actual renewable fraction somewhat when we allow consumption to grow to a larger target value.

An alternative to the one percent strategy is to increase the amount of renewable resources exponentially. Throughout my discussion, I have been using the terms “renewable resources” and “capacity” interchangeably, where they are both defined as the amount of resources we are able to use that is replenished on an annual basis. Capacity is more rigorously defined as the capability of replenishing a maximum amount of resources, where the amount of renewable resources actually consumed increases until the capacity is reached; any additional consumption is supplied by non-renewable resources. If we want to supply more renewable resources (reduce the drain on non-renewable resources) then we must increase capacity; and if we want to do it fast, exponential growth is a natural way to go.

My combined population model achieves its lowest amount of error in calculating historical population (from 0 A.D.) when the capacity is zero. Because the original amount of resources is large (1.7 quadrillion pounds), even a capacity equal to the initial consumption of 300 million pounds results in a fraction of a percent increase in error. The capacity is unlikely to be larger than the amount calculated from the world ecological footprint, which I estimate to be 6.9 trillion pounds; this amount results in a 2% increase in error for 2005, which is too large to accept. The smallest the capacity could be (other than zero) is perhaps the 100 pounds per person estimated to be consumed annually in 0 A.D. (roughly the weight of a person).

When dealing with exponential growth, the starting value has a critical impact on the growth rate required to reach a final value in a given amount of time. If the world were to start increasing capacity in 2010, the rate the model predicts would be necessary to avoid population collapse varies from 9% (for a starting capacity of 300 million pounds) to 52% (with a starting capacity of 100 pounds); if the capacity were 6.9 trillion pounds, the rate would be less than half a percent. Given the stakes, I would argue for using the 52% rate if the one percent strategy was impractical (where the fraction of total consumption supplied by renewable resources is increased by 1% per year). Of course in both cases consumption must ultimately be limited to a maximum amount, which is much more likely to draw resistance than a position on the appropriate growth rate.

If we depend on Nature for renewable resources (the easiest approach to growing capacity, since the “technology” is already available), and its physical limit is the maximum capacity I mentioned, we will at best be able to support the population we had in 1980 (4.5 billion people). The rest, nearly one and a half times more, will need to come from us.

Version 2

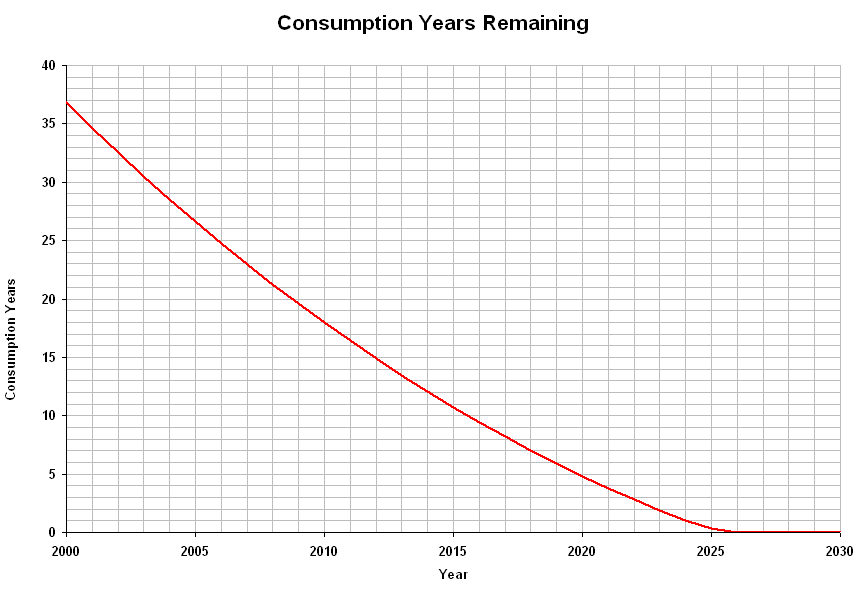
A refined version of the population-consumption model shows the population peak occurring in 2021, with the population crashing to zero by 2027. In this version, either the ratio of renewable resource consumption to total consumption must rise at a rate of 3% per year starting at the end of 2008, or capacity (beginning at 100 lb) must triple each year to avoid population collapse.

[Note: This article is an edited and updated combination of related posts to the Idea Explorer blog.]