Fixing The Unknown
Fixing a problem, like completion of a task, often assumes that the problem is well-defined (known). In reality there will also be an unknown component of the problem that must be found and then fixed.
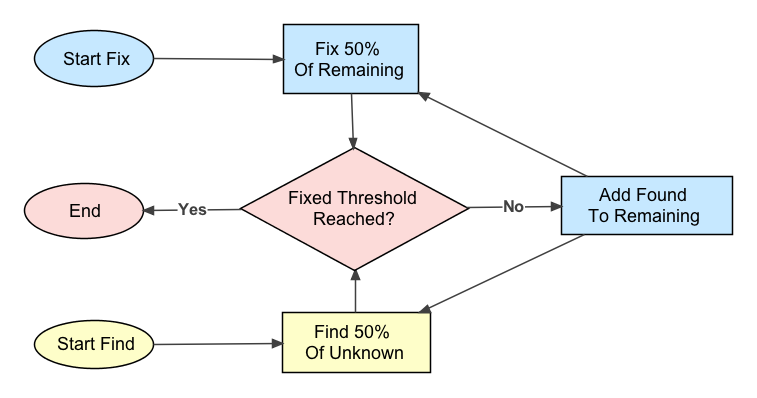
Following is a flowchart of this process, which stops when a certain fraction of the problem has been fixed (minimum completion, or "fixed threshold").
Both fixing and finding are done with a degree of efficiency, which determines how much of the remaining task will be completed in an interval of time equal to the ideal needed to complete the task (with 100% eficiency). A typical efficiency is 50% for someone who already has the basic requisite skills.
In this process, two people or groups (depending on the size of the problem) are each providing a unit of "effort" per unit of ideal time, for a total of two units of effort during each interval.
.png)
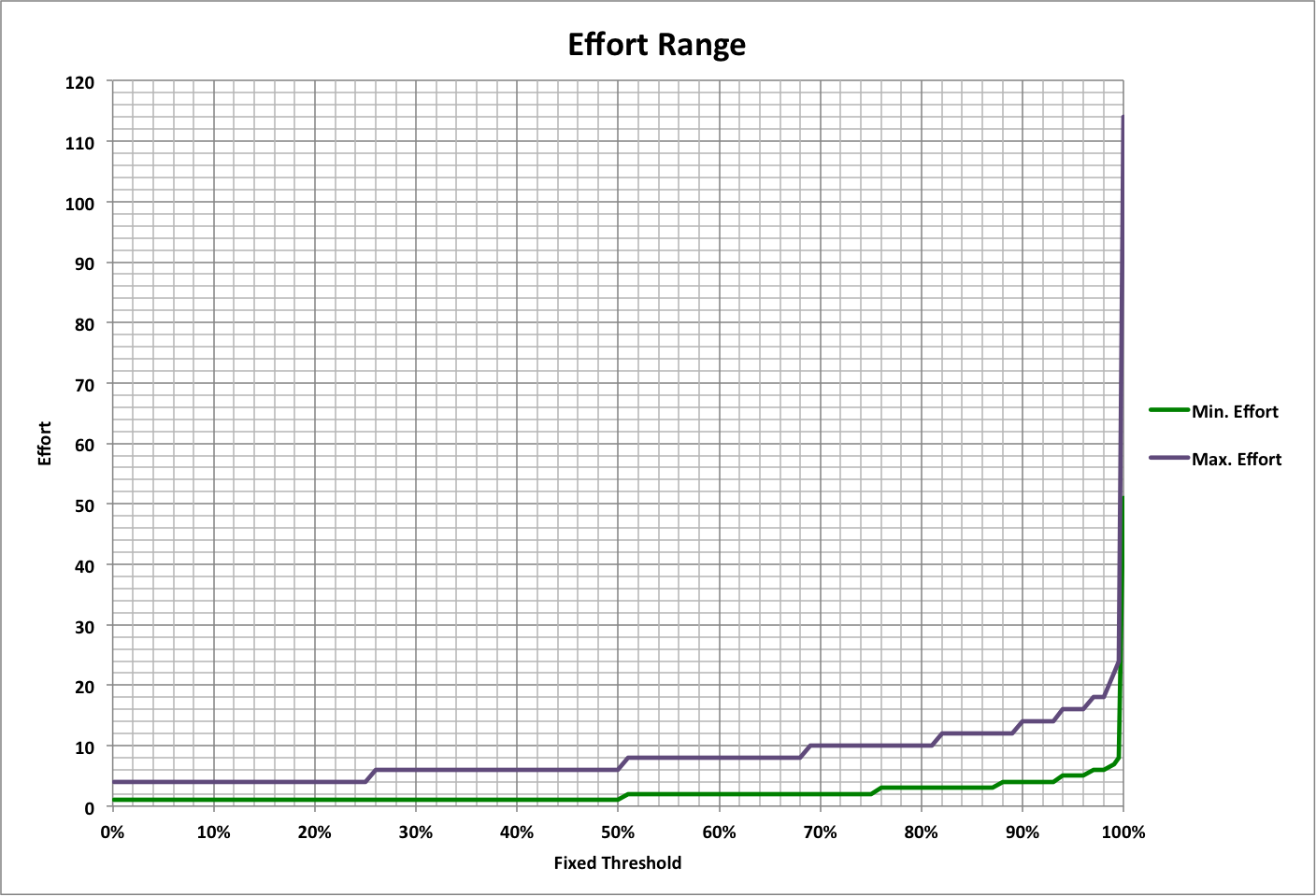
The amount of the problem that is unknown determines how soon as the fixed threshold is reached or exceeded, as shown in the following graph where the amount is represented by the ratio of the unknown part to the known part. As above, the efficiencies for both fixing and finding are assumed to be 50%, and time is in units of ideal time.
In each case, there are maximum values for time and effort that apply for all higher ratios of unknown to known.
.png)
See also:
- Normal Completion
- Responsible Problem Management (Blog Post)